2/3; 2
Объяснение:
3y^2-8y+4=0
D=(-8)^2-4*3*4=64-48=16
В уравнении 2 корня, значит
x1 = (-(-8) +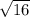 
)/(2*3) = 12/6 = 2 - первый корень
x2 = (-(-8) - 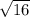)/(2*3) = 4/6 = 2/3 - второй корень
Как найти дискриминант?
1) Дискриминант квадратного уравнения ax^2+bx+c находится по формуле: b^2-4ac. a; b и c - коэффициенты. В данном случае a=3; b=-8; c=4.
2) Подставляем: D=(-8)^2-4*(3*4)=64-48=16
3) Если D>0, то в уравнении 2 корня, если D=0, то в уравнении 1 корень, если D<0, то в уравнении корней нет
Как найти корни?
Опять же таки берём уравнение вида ax^2+bx+c
Если D>0, то x1 = (-b+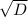
)/2a
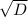x2 = (-b-)/2a
Если D=0, то x = -b/2a
Если D<0, то ничего не ищем
P.S. Также есть теоремы Виета и выделения полного квадрата, но они более замороченные. Конечно, проще решать через дискриминант, но если вы хотите увидеть, как решить уравнение другим напишите, я отредактирую ответ, попробую решить другим
ΔАВС , СН⊥АВ , СК - медиана ⇒ АК=ВК=1/2*АВ , ∠АСН=∠КСН=∠ВСК
S(ΔАВС)=1,5+√3 . Найти радиус вписан. окружности r .
Так как СН - высота и ∠АСН=∠КСН, то СН - биссектриса. А если в треугольнике биссектриса является ещё и высотой, то это возможно только в равнобедренном треугольнике. Но по свойству равноб. треуг. СН ещё и медиана равнобедренного ΔАСК . Значит, АН=НК.
НК=АН=1/2*АК=1/2*ВК=1/2*(с/2)=с/4 ( обозначения АВ=с , АС=b , ВС=а ) .
Рассм. ΔВСН, ∠ВНС=90° , ВН=ВК+НК=с/2+с/4=3с/4
Проведём КР⊥ВС ⇒ ∠КРС=90° .
ΔКСН=ΔКСР , так как у этих прямоугольных треугольников имеется общая гипотенуза СК и равные острые углы ∠КСН=∠КСР ⇒
КН=КР=с/4
В ΔВКР катет КР=с/4 , а гипотенуза ВК=с/2. То есть катет в 2 раза меньше гипотенузы, значит угол, лежащий против катета КР равен 30° ⇒ ∠В=30° .
Из ΔВСН найдём ∠ВСН=180°-∠ВНС-∠В=180°-90°-30°=60°
Так как ∠ВСН=∠ВСН+∠КСН , а ∠ВСН=∠КСН , то ∠ВСН=∠КСН=60°:2=30° ⇒ ∠АСН=30° ⇒ ∠АСВ=3*30°=90°
ΔАВС - прямоугольный
Радиус вписанной окружности в прямоугольный треугольник равен
Так как в ΔАВС: ∠В=30° , то АС=1/2*АВ , то есть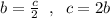
.
Найдём площадь ΔАВС.