8 км/ч
Объяснение:
Пусть V - скорость первого бегуна, S - второго, а К - длина круга. Запишем условие задачи в алгебраическом виде:
V/4 + 1 = K
S/6 = K
V + 10 = S
приравняем К и получим из первых двух уравнений одно:
V/4 + 1 = S/6
Подставим вместо S -> V+10, получим:
V/4 + 1 = (V+10)/6
(V + 4)/4 = (V+10)/6
3*(V+4) - 2*(V+10) = 0
3V + 12 - 2V - 20 = 0
V = 8
(для проверки можете посчитать также S = V + 10 = 8 + 10 = 18; а также K = S/6 = 18/6 = 3. Если V = 8, то K = V/4 + 1 = 2+1 = 3, то есть задача решена верна, но условие от нас проверки и всех этих расчетов не требует).
Для первой пары уравнений координаты пересечения: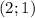 
, для второй пары: 
.
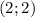Объяснение:
Нам требуется найти координаты точек пересечения графиков уравнений, без построения самих графиков. Для этого надо объединить два уравнения, которыми заданы графики, и объединить их в систему уравнений:
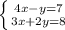
Данную систему уравнений проще решить методом подстановки одной переменной в другое уравнение. Из первого уравнения выражаем переменную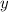 
, перенеся её в правую сторону уравнения, а 7 переносим в левую сторону, меняя знак на противоположный:
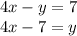
Теперь подставляем значение 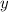во второе уравнение:
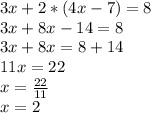
Теперь находим 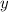, подставляя значение 
обратно в первое уравнение системы:
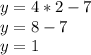
Получаем, что координата точек пересечения этих двух графиков является .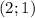
Таким же объединяем другие уравнения в систему уравнений:
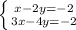
В данном случае проще выразить из первого уравнения и подставить данное значение во второе уравнение:
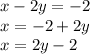
Теперь подставляем данное значение во второе уравнение системы, перенося неизвестные значения в левую сторону, а известные в правую:
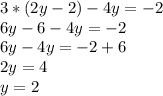
Возвращаемся в уравнение для , подставляя значение 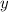, получаем:
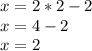
Получили, что координата точек пересечения данных графиков является пара .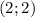
Объяснение:
8х²+2x+5=0
D=2²-4*8*5=4-160=-156
ответ: D=-156.