Производную надо скорее знать, чем понимать, то есть с заученными правилами ты без проблем сможешь решить любую задачку на производную. Во вложениях я оставлю некоторые правила дифференцирования и прозводные некоторых элементарных функций.
Но вернемся к нашим баранам. Задача 2.
f=(1+2x)/(1-2x). По правилу производной от частного:
f'=((1+2x)' * (1-2x) - (1-2x)' * (1+2x)) / (1-2x)^2 =
=(2*(1-2x) - (-2)*(1+2x)) / (1-2x)^2 =
= (2-4x+2+4x) / (1-2x)^2 = 4 / (1-2x)^2
Итого f'(0)=4/(1-0)^2 = 4.
Задача 4.
f=ln(sqrt(x^2+1))
По свойству производной от логарифма:
f' = (sqrt(x^2+1))' / sqrt(x^2+1)
По свойству производной от корня (рассмотрим только числитель):
g' = (sqrt(x^2+1))' = ((x^2+1)^(1/2))' = (1/2) * (1/sqrt(x^2+1)) * (x^2+1)'
Ну и оставшаяся производная равна
h' = (x^2+1)' = 2x
Итак, собираем все вместе:
f' = g'/sqrt(x^2+1) = h'/(2*(x^2+1) = x/(x^2+1)
Фух, теперь ищем желанное f'(1):
f'(1)=1/(1+1)=1/2
Ну вот вроде и все, если будут вопросы - пиши, попытаюсь ответить.
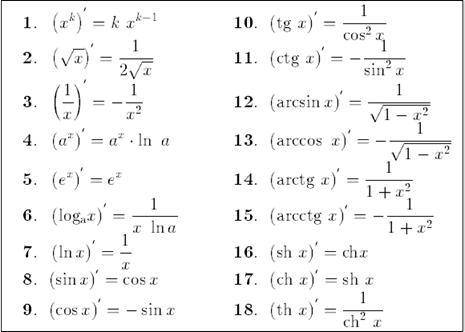

0<x<4/3
Объяснение:
числитель является положительным (это число 7, от x не завист)
надо найти значения x, при которых знаменатель положителен:
4 × x - 3 × x**2 > 0
4 × x - 3 × x**2 = x × (4 - 3×x)
рассмотрим 2 случая:
1. Оба положительные ( и x, и (4 - 3×x)): одновременно должно выполняться:
x > 0 и 4 - 3 × x > 0
x > 0 и -3×x > -4
x > 0 и x < 4/3
в этом случае решение существует. А именно,
0<x<4/3
2. Оба отрицательные: одновременно должно выполняться:
x < 0 и 4 - 3×x < 0
x < 0 и -3 × x < - 4
x< 0 и x> 4/3
в этом случае решения не существует.
Оставляем первый случай.
4x+24=24
4x=0
X=0