а) Выбрать 4 ромашки можно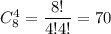 
а 3 незабудки - 
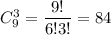По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно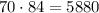 
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно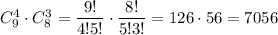 
Выбрать пять незабудки и две ромашки можно 
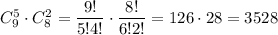Выбрать шесть цветов незабудки и одна ромашку можно 
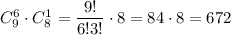И наконец выбрать семь цветов незабудки можно 
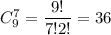По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
ответ: 11292.
x3+x−2=0
x3+x−2=0Ищем первый корень через делители числа -2.
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .Приравниваем его к нулю, видим, что корней нет, так как дискриминат отрицательный.
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .Приравниваем его к нулю, видим, что корней нет, так как дискриминат отрицательный.Следовательно, ответ: x=1
Объяснение:
16x+14y=64 при y=0
подставляем 0 в уравнение,получается:
16x+14*(0)=64 (14*0=0)
16x+0=64
16x=64
x=64/16
x=4
ответ:4