Решить неравенства методом интервалов.
Объяснение:
1) (х+7) (х+5 )(х-9)≤0
Найдем нули : х+7=0 →х=-7 ; х+5=0 →х=-5 ; х-9=0 →х=9.
Метод интервалов - + - +
-7-59
( кружочки около чисел закрашенные) .Определяется знак любого промежутка , далее знаки чередуются, т.к. каждый множитель данного неравенства нечетной степени. Я брала х=0 ( третий промежуток) . Значение левой части отрицательно.
Выбираем промежутки , где стоит знак "-".
х∈ (-∞ ; -7] ∪ [-5;-9]
3)(х²-64)(х²+10х+9)≥0.
Разложим на множители х²+10х+9 применив т. Виета : х₁+х₂=-10 , х₁*х₂=9 ,х₁=-1,х₂=-9. Получим х²+10х+9=(х+1)(х+9).
Разложим на множители х²-64 по формуле разности квадратов :
х²-64=(х-8)(х+8).
Получили неравенство (х-8)(х+8)(х+1)(х+9)≥0
Нули каждой скобки : -9, -8, -1, 8. Кружочки на схеме закрашены .
Метод интервалов : При х=0, знак 4 промежутка "-". Все знаки чередуются , т.к. каждый множитель данного неравенства нечетной степени.
+ - + - +
-9 -8 -1 8
Выбираем те , где знак "+". х∈ (-∞ ; -9] ∪ [-8;-1]∪ [8;+∞)/
7)(3-х)²(х+2)²(х-1) (2x-5)<0.
Нули каждой скобки : -2; 1; 2,5 ; 3. Кружочки на схеме НЕ закрашены .
Метод интервалов : При х=0, знак 2 промежутка "+". Знаки чередуются только у значений нечетной степени. Около значений скобок четных степеней не чередуются ( т.е около чисел -2 и 3)
- - + - -
-2 1 2,5 3
Выбираем те , где знак "-". х∈ (-∞ ; -2) ∪ (-2; 1) ∪ (2,5;3) ∪ (3;+∞)
1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
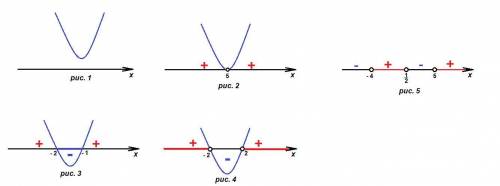
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
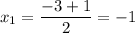
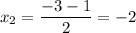
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
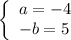 или
или 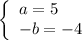
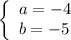 или
или 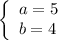
ответ: a = - 4, b = - 5 или a = 5, b = 4.
1.)х =15
у = 5
2.) х=2
у=2
3)х = 8.3
у=4
4)х=10
у=14
Объяснение: