18 – 8х^2

х^8 – у^4

у^2 – в^2 – 12в – 36

30 + 3ху – 15у – 6х

Разложить на множители

Question

Алгебра: 18 – 8х^2 х^8 – у^4 у^2 – в^2 – 12в – 36 30 + 3ху – 15у – 6х Разложить на множители

dasha00097 · Accepted Answer

Нехай у першому випадку теплохід пройшов за течією

км, тоді проти течії — 222-x

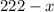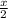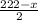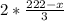км. Швидкість, з якою він тоді йшов, за течією складала $\frac{x}{2}$ км/год, а проти течії — $\frac{222-x}{2}$ км/год. Тоді у другому випадку теплохід пройшов за течією $3*\frac{x}{2}$ км, а проти — $2* \frac{222-x}{3}$ км, що за умовою на 60 км більше. Маємо рівняння: (перше фото).
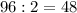З отриманої відстані знайдемо швидкість теплохода за течією у першому випадку: 96:2=48

км/год і швидкість проти течії: 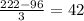$\frac{222-96}{3} =42$ км/год. Нехай власна швидкість теплохода

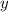км/год, а течії —

км/год. Маємо систему:
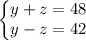
$\left\{\begin{matrix}
y+z=48\\ 
 y-z=42& & 
\end{matrix}\right.$
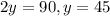Додамо до першого рівняння друге, маємо: 2y=90, y=45

км/год.

Відповідь: 45 км/год.

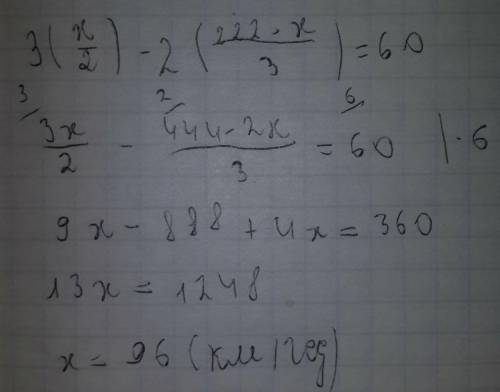
Теплохід проходить за 2 години за течією річки і 3 години проти течії 222км.він же за 3 години за те

18 – 8х^2х^8 – у^4у^2 – в^2 – 12в – 3630 + 3ху – 15у – 6хРазложить на множители

MOGZ ответил

18 – 8х^2

х^8 – у^4

у^2 – в^2 – 12в – 36

30 + 3ху – 15у – 6х

Разложить на множители