y=3/35
Объяснение:
120y+4=13+15y
120y-15y=13-4
105y=9
y=3/35
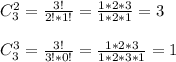
1 задание. 5х-у-2=0
х в квадрате -2ху+у в квадрате=0
-у=2-5х
х в квадрате -2ху+у в квадрате=0
у=5х-2
х в квадрате-2ху+у в квадрате=0
х в квадрате-2х(5х-2)+(5х-2) в квадрате=0
х в квадрате -10х в квадрате +4х+25х в квадрате +4-20х=0
16х в квадрате -16х+4=0
Д=16 в квадрате -*16*4=256-256=0
х=16/(4*16)=0,25
у=5*0,25-2=1,25-2=-0,75.
ответ: х= 0,25; у=-0,75
Объяснение: