Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
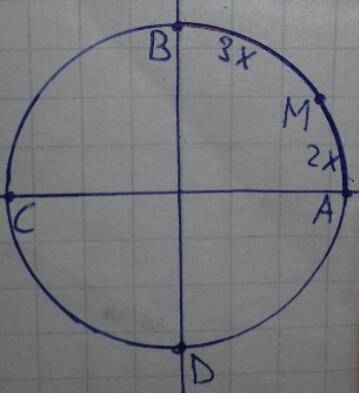
∪AC = π = 2·∪AB ⇒ ∪AB = 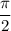
Пусть ∪AM =  , тогда ∪MB =
, тогда ∪MB = 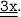
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x = 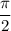 ⇒
⇒
x = 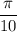 ⇒
⇒ 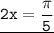 ;
; 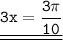
∪DM = ∪DA + ∪AM = 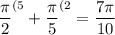
∪MC = ∪MB + ∪BC = 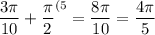
ответ: длина ∪AM = 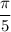
длина ∪MB = 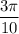
длина ∪DM = 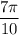
длина ∪MC = 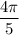
0
Объяснение:
Не очень понял. Возможно что это уравнение?
2^x+2^(-x)=2cos2x
Используем неравенство между средним арифметическим и средним геометрическим для двух положительных чисел 2^x и 2^(-x), а также то что cos2x≤1
2≥2cos2x=2^x+2^(-x)≥2·√(2^x·2^(-x))=2
Равенство возможно только при
2cos2x=2 и 2^x=2^(-x)
2^x=2^(-x)⇒2^(2x)=1⇒2x=0⇒x=0
При x=0 ⇒2cos2x=2cos0=2