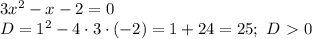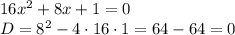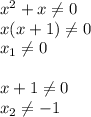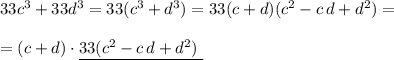
а) p(x) = x² - 10x + 5 = x² - 10x + 25 - 20 =(x - 5)² - 20.
Поскольку (x - 5)² ≥ 0, тогда наименьшее значение выражения (x - 5)² - 20 равно -20.
б) p(x) = 2x² - 6x + 3 = 2(x² - 3x + 1,5) = 2(x² - 3x + 2,25 - 0,75) = 2(x - 1,5)² - 1,5.
Поскольку 2(x - 1,5)² ≥ 0, тогда наименьшее значение выражения 2(x - 1,5)² - 1,5 равно -1,5.
в) p(x) = x² - 5x + 8 = x² - 5x + 6,25 + 1,75 =(x - 2,5)² +1,75.
Поскольку (x - 2,5)² ≥ 0, тогда наименьшее значение выражения (x - 2,5)² + 1,75 равно 1,75.
г) p(x) = 3x² + x = 3(x² + 1/3x) = 3(x² + 2/6x + 1/36 - 1/36) = 3(x + 1/6)² - 1/12.
Поскольку 3(x + 1/6)² ≥ 0, тогда наименьшее значение выражения 3(x + 1/6)² - 1/12 равно - 1/12.
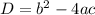 (если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена
(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена