Пояснение:
Это квадратное уравнение можно решить сразу тремя : через теорему Виета и через Дискриминант (полный и краткий). Покажу все три.
(теорема Виета)
- можно применять, если первый (старший) коэффициент (а) равен единице (1), то есть квадратное уравнение имеет вид:
x² ± px ± q = 0.
x² + 8x + 15 = 0
p = 8; q = 15.
По т. Виета:
x₁ + x₂ = - 8,
x₁ × x₂ = 15.
x₁ = - 5,
x₂ = - 3.
<><><><><><><><><><><><><><><><>
IIа (Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
ax² ± bx ± c = 0.
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
D = b² - 4ac = 8² - 4 × 1 × 15 = 64 - 60 = 4 = 2².
D > 0 (значит, уравнение имеет два действ. корня)
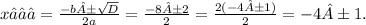
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
IIб ("краткий" Дискриминант)
- можно применять к любым полным квадратным уравнениям вида:
- можно применять к любым полным квадратным уравнениям вида:ax² ± bx ± c = 0,
где b - чётное число (то есть делится на 2 без остатка).
x² + 8x + 15 = 0
a = 1; b = 8; c = 15.
k = b ÷ 2 = 8 ÷ 2 = 4.
D₁ = k² - ac = 4² - 1 × 15 = 16 - 15 = 1.
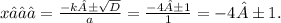
x₁ = - 4 - 1 = - 5,
x₂ = - 4 + 1 = - 3.
<><><><><><><><><><><><><><><><>
ответ: - 5; - 3.
Удачи Вам! :)
Объяснение:
Находим границы фигуры, приравняв функции:
x² - 4 = -x - 2.
Получаем квадратное уравнение х²+ х - 2 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=1^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√9-1)/(2*1)=(3-1)/2=2/2=1;x_2=(-√9-1)/(2*1)=(-3-1)/2=-4/2=-2.
Искомая площадь фигуры равна интегралу:
S= \int\limits^1_{-2} {(-x-2- x^{2} +4} \, dx = \int\limits^1_{-2} {(- x^{2} -x+2)} \, dx =- \frac{x^3}{3}- \frac{ x^{2} }{2}+2x|_{-2}^1S=−2∫1(−x−2−x2+4dx=−2∫1(−x2−x+2)dx=−3x3−2x2+2x∣−21
Подставив пределы, получаем: S =((-1/3)-(1/2)+2*1) - ((8/3)-4/2+2*(-2)) =
= (7/6)-(-10/3) = 9/2 = 4,
9ГШАЦЩАШЦШЩКУГШЩКШЩНЕ
Объяснение:ПЕАПЕА
АПТЬЛОРПАЫПЮ.