y=x³-6x²+9 на отрезке [ -1;5 ]
Область определения х-любое.
1)Промежутки возрастания и убывания.
у'=(х³-6х²+9)'=3х²-12х=3х(х-4)=3.
Критические точки х=0,х=-4 , при у'=0.
у'>0. , 3х(х-4)>0
(0)(4) , возрастает при х∈(-∞; 0) и ( 4;+∞) .
Т.к. функция определена и непрерывна при любом х, то можно включит концы отрезка х∈(-∞; 0] и [ 4;+∞)
Если у'<0 . то функция убывает .
Используя схему выше ⇒ х∈[ 0; 4] .
2)Экстремумы.
у' + - +
(0)(4)
у возр max убыв min возр
х=0 точка максимума , у(0)=y=0³-6*0²+9=9
х=4 точка минимума , у(4)=4³-6*4²+9=- 23
![С производной построить график функции на отрезке [ -1;5 ] y=x^3-6x^2+9](/tpl/images/4510/6934/0781c.jpg)


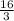
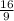
 или х₂ = 1
или х₂ = 1
Пусть х км/ч - собственная скорость лодки, тогда (х + 1) км/ч - скорость лодки по течению реки, (х - 2) км/ч - скорость лодки против течения реки. Уравнение:
24/(х+1) + 12/(х-1) = 5
24 · (х - 1) + 12 · (х + 1) = 5 · (х + 1) · (х - 1)
24х - 24 + 12х + 12 = 5 · (х² - 1²)
36х - 12 = 5х² - 5
5х² - 5 + 12 - 36х = 0
5х² - 36х + 7 = 0
D = b² - 4ac = (-36)² - 4 · 5 · 7 = 1296 - 140 = 1156
√D = √1156 = 34
х₁ = (36-34)/(2·5) = 2/10 = 0,2 - не подходит по условию задачи
х₂ = (36+34)/(2·5) = 70/10 = 7 км/ч - скорость лодки
Вiдповiдь: 7 км/год - власна швидкiсть човна.