Question

с ответом...алгебра и не надо писать всякую чушь

Answer 1

Объяснение:

№1

a) x–x²=0

Д= 1–4*0*(–1)= 1

х(1)=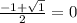 $\frac{ - 1 + \sqrt{1} }{2} = 0$

х(2)=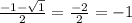 $\frac{ - 1 - \sqrt{1} }{2} = \frac{ - 2}{2} = - 1$

б) 4у²–у=0

Д= 1–4*0*4=1

у(1)=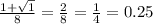 $\frac{1 + \sqrt{1} }{8} = \frac{2}{8} = \frac{1}{4} = 0.25$

у(2)=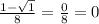 $\frac{ 1 - \sqrt{1} }{8} = \frac{0}{8} = 0$

№2

а) 8а³–b³+4a²+2аb+b²= (2а–b)(4a²+2ab+b²)+(4a²+2аb+b²)= (4a²+2ab+b²)(2a–b+1)

б) 8а³–b³+4a²–4ab+b²= (2а–b)(4a²+2ab+b²)+(2a–b)²= (2a–b)(4a²+2ab+b²+2a–b)

c) –a²+8ab–16b²= –(a–4b)²