ТЕСТ ПО ТЕМЕ «РЕШЕНИЕ ЛИНЕЙНЫХ НЕРАВЕНСТВ» 8 КЛАСС ВАРИАНТ № 1
1. Какое из чисел является решением неравенства 3х > х + 3?
1) - 1; 2) 2; 3) 0; 4) -2.
2. Неравенству х < 5 соответствует промежуток
1) ( - ∞; 5]; 2) [5; +∞); 3) ( - ∞; 5); 4) (5; +∞).
3. Решите неравенство 3х < 18
1) ( - ∞; 6]; 2) [6; +∞); 3) (6; +∞); 4) ( - ∞; 6).
4. При каких значениях х значение выражения - 4х меньше 20?
1) ( - ∞;-1/5); 2) (-1/5; +∞); 3) ( - ∞; -5); 4) (-5; +∞).
5. Решите неравенство 3(х – 2) ≤ 6х – 4
1) [-2/3;+∞); 2) (- ∞; -2/3]; 3) (- ∞; -3/2]; 4) [-3/2;+∞) .
6. При каких значениях х выражение (6-2х)/4 принимает неотрицательные значения?
1) [3; +∞); 2) ( - ∞; 3]; 3) [ 1/3;+∞); 4) (- ∞; 1/3 ].
7. Решите неравенство х/4+ х/2<6
1) (8; +∞); 2) ( - ∞; 8]; 3) [8; +∞); 4) ( - ∞; 8).
8. Решите неравенство (3х-2)/4 + (4х+1)/3 ≥0
1) [12,5; +∞); 2) ( - ∞; 12,5]; 3) ( - ∞; 0,08]; 4) [0,08; +∞).
9. Укажите наибольшее целое решение неравенства 3(х – 6) – 2(х + 8) < 7
1) 41; 2) 40; 3) 1; 4) 42.
10. Укажите наименьшее целое решение неравенства (3с-2)/6 ≤ (4+5с)/3
1) 1; 2) -2; 3) -1; 4) 0.
11. При каких значениях х имеет смысл выражение √(12-3х) ?
1) ( - ∞; 4); 2) (4; +∞); 3) [4; +∞); 4) ( - ∞; 4].
12. Решите неравенство 6(3 – 2х) + 3(4х – 2) ≥ 0
1) х ≥ 0; 2) нет решений; 3) х – любое число; 4) х ≥ -12.
С решением
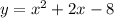
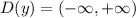
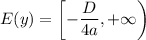 - где D дискриминант.
- где D дискриминант.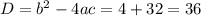
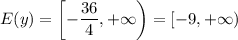
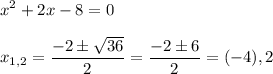
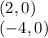



![(-\infty,-1]](/tpl/images/0467/5865/91666.png)
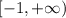

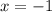
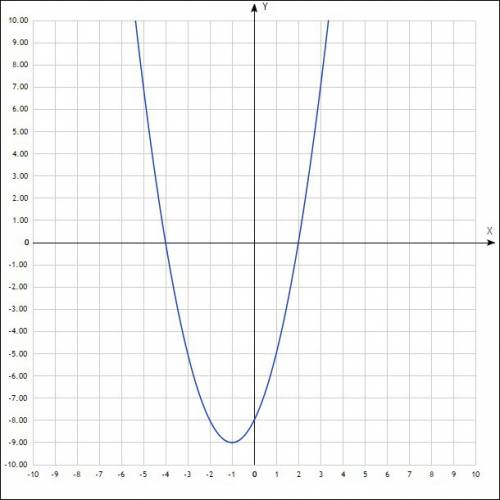
2. (b-5)(b+10)+(b+6)(b-8)=b²+10b-5b-50+b²+6b-8b-48=2b²+3b-98
Задача
1) 26 * 3 = 78 деталей сделали вдвоём за 3 часа
2) 5 – 3 = 2 часа работал первый дополнительно
3) 108 – 78 = 30 деталей – сделал первый рабочий за 2 часа
4) 30 : 2 = 15 деталей изготавливал ежечасно первый рабочий.
5) 26 – 15 = 11 деталей изготавливал ежечасно второй рабочий.
ответ: 15 дет. ; 11 дет.
Проверка
15 * 5 + 11 * 3 = 108
75 + 33 = 108
108 = 108 верно