ответ: рисунок В .
Уравнение прямой имеет вид y = kx + b .
Чтобы определить, на каком рисунке начерчена прямая y = -2x - 2 , надо обратить внимание на коэффициент перед переменной х .
k= -2 < 0
Так как k<0 , то прямая будет наклонена к положительному направлению оси ОХ под тупым углом . Это видно на рисунке Б и В .
Значит рисунки А и Г не рассматриваем .
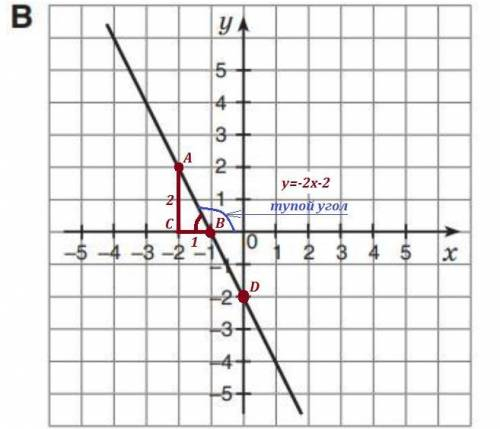
Чтобы убедиться, что k= -2 , строим прямоугольный ΔАВС , ∠С=90° .
Точка В - точка пересечения прямой и оси ОХ , точка А - узловая точка на прямой . Находим отношение АС/ВС=2/1=2 . Значит, действительно коэффициент равен 2 с минусом , то есть k= -2 .
( Минус добавляем из-за того, что угол наклона тупой . )
Теперь определим свободный член . По условию он равен b= -2 . Значит ордината точки пересечения прямой с осью ОУ должна быть равна -2 .
На чертеже точкa пересечения прямой с осью ОУ - это точка
D( 0 ; -2 ) имеет ординату, равную -2 . ( Кстати, на чертеже Б
ордината точки пересечения прямой с осью ОУ равна 2, поэтому
этот рисунок не годится . )
Замечание . На рис. А - прямая у= 2х-2 , на рис. Б - прямая у= -2х+2 ,
на рис. Г - прямая у=2х+2 .
ответ: А) 1
Объяснение:
a₂ = a₁ + d
a₃ = a₁ + 2d
Складемо систему рівнянь:
{a₁ + a₂ + a₃ = 2
{a₁² + a₂² + a₃² = 14/9
{a₁ + a₁ + d + a₁ + 2d = 2
{3a₁ + 3d = 2 | :3
{a₁ + d = 2/3
a₂ = 2/3
Підставимо у друге рівняння a₂ = 2/3
{a₁² + (2/3)²+ a₃² = 14/9
{a₁² + 4/9 + a₃² = 14/9
a₁² + a₃² = 14/9 - 4/9
a₁² + a₃² = 10/9
a₁² + (a₁ + 2d)² = 10/9
a₁² + a₁² + 4a₁d + 4d² = 10/9
2a₁² + 4a₁d + 4d² = 10/9 | :2
a₁² + 2a₁d + 2d₁² = 5/9
a₁² + 2a₁d + d² + d² = 5/9
(a₁ + d)² + d² = 5/9
a₂² + d² = 5/9
(2/3)² + d² = 5/9
4/9 + d² = 5/9
d² = 5/9 - 4/9
d² = 1/9
d = ± 1/3
Звідси знайдемо третій член прогресії:
d = 1/3
a₁ = a₂ - d = 2/3 - 1/3 = 1/3
a₃ = a₁ + 2d = 1/3 + 2 * 1/3 = 1/3 + 2/3 = 3/3 = 1
Во втором - последнее x=п/4+пn
Объяснение: