242
Объяснение:
Наименьшее возможное значение суммы трёх неравных членов равно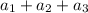 
, наибольшее значение суммы двух членов равно 
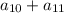. Значит, если для этих членов неравенство выполняется, то и для любых других гарантированно выполняется.
Два соседних числа отличаются как минимум на 1, значит,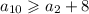 
и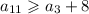 
.
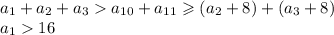
Наименьшее значение первого члена 17, тогда следующий член не меньше 18, третий - не меньше 19 и т.д.
Наименьшая сумма отсюда равна
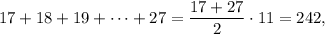
если, конечно, последовательность 17, 18, ..., 27 удовлетворяет условию
Легко проверить, что эта последовательность подходит: действительно, 17 + 18 + 19 = 54 > 53 = 26 + 27
Объяснение:
Выполним преобразование:
Пусть![\sqrt{x+y}=k,\;\sqrt[3]{x-y}=t](/tpl/images/1358/0734/e7517.png)
.
Тогда для 1-ого случая:
Заметим здесь теорему Виета (если не заметили, то можно просто решить эту систему).
Тогда:
или
Замечу, что замену можно было не делать. Она дана для понимания. Можно было сразу написать то, что идет после слов обратная замена.
Обратная замена:
Первое уравнение можно возвести в квадрат, так как обе части его положительны:
Очевиден прием решения: сложение.
Получили пару чисел (12; 4).
Получили пару (34; -30).
Для 2-ого случая:
Еще одна пара чисел: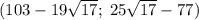
Заметим, что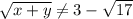
, т.к. это число меньше 0.
Система уравнений решена!