Имеем бесконечно убывающую геометрическую прогрессию, |q| < 1
b2 = b1*q
b1 = b2/q
Нам нужно найти знаменатель бесконечно убывающей прогрессии, у которой второй член в 8 раз больше сумма всех ее последующих членов. То есть нам нужно знать две суммы: всей геометрической прогрессии и её части - от третьего члена до бесконечности.
S1 = b1/1-q - сумма всей геометрической прогрессии
S2 = b3/1-q - сумма членов геометрической прогрессии, начиная с третьего.
b2 = 8*S2 - второй член в 8 раз больше суммы всех членов, начиная с третьего.
Немного поработаем с формулами:
b2 = 8*S2
b1*q = 8 * b1*q^2/1-q
b1*q(1-q) = 8*b1*q^2
q - q^2 = 8*q^2
q - 9q^2 = 0
q(1-9q) = 0
q = 0 и 1-9q = 0
q = 1/9
q не может быть равно нулю(это одно из условий в геометрической прогрессии). Поэтому ответ один - 1/9.
=)
1) 20 мин = 1/3 часа
2) 1 - 1/3 = 2/3 расстояния Коля проходит пешком со скоростью 4,8 км/ч за 1/3 часа
3) 4,8 · 1/3 = 1,6 км - это 2/3 расстояния от дома до школы.
4) 1,6 : 2 · 3= 2,4 км - расстояние от дома до школы
5) 2,4 : 3 · 1 = 0,8 км - расстояние, которое Коля пробегает со скоростью 16 км/ч
6) 0,8 км : 16 км/ч = 0,05 часа - время, за которое Коля пробегает 1/3 часть всего расстояния
7) 0,05 ч + 1/3 ч=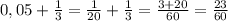
= 23 мин - время Коли на весь путь
8) 2,4км : 6 км/ч = 0,4 ч = 24 мин - время Вити на весь путь
9) 24 мин - 23 мин = 1 мин
ответ: а) 2,4 км - расстояние от дома до школы ;
б) на 1 минуту Коля приходит в школу раньше Вити.