Функция у = х² + 4х - 12
График функции - квадратная парабола веточками вверх
Найдём характерные точки этой параболы.
1) Точка пересечения с осью Оу: х = 0; у = -12;
2) точки пересечения с осью Ох: у = 0
х² + 4х - 12 = 0
D = 4² - 4 · (-12) = 64
√D = 8
x₁ = (-4 - 8)/2 = -6
x₂ = (-4 + 8) = 2
Получили две точки (-6; 0) и (2; 0)
3) найдём координаты вершины С параболы С(m; n)
m = - b/2a = -4/2 = -2
n = y(-2) = (-2)² + 4 · (-2) - 12 = -16
C(-2; -16)
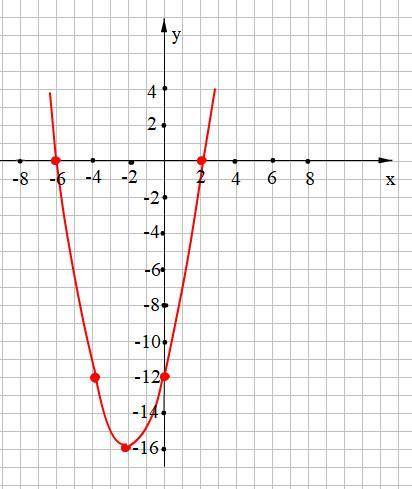
По найденным точкам строим параболу (смотри прикреплённый рисунок).
По графику находим
а) у > 0 при х ∈ (-∞; -6)∪(2; +∞); y < 0 при х ∈ (-6; 2)
б) у↑ при х ∈ (-2; +∞); у↓ при х ∈ (-∞; -2)
в) у наим = у(-2) = -16; наибольшего значения не существует.
2a-1
10a^{2} -a-2
Мы знаем, что дробь равна нулю, когда числитель равен нулю, а знаменатель - нет.
10а^{2} -a-2\neq 0
Разложим знаменатель на множители, для того, чтобы увидеть: можно ли сократить дробь. А для того, чтобы разложить на множители, мы знаменатель приравняем к нулю и найдём корни квадратного уравнения.
10а^{2} -a-2=0
D=b^{2} -4ac
D=1-4*10*(-2)=1+80=81
\sqrt{D} = \sqrt{81} = 9
a_{1} = 1+9 = 10 = 1 = 0,5
2*10 20 2
a_{2} = 1-9 = -8 = -2 = -0,4
2*10 20 5
Разлаживаем на множители: 10*(a-0,5)(a+0,4).
Теперь подставляем разложеный на множители знаменатель в дробь, а в числителе выносим общий множитель 2 (чтобы мы смогли сократить дробь.
2*(a-0,5)
10*(a-0,5)(a+0,4)
Сокращаем дробь на множитель (a-0,5) - у нас остаётся 1, и на множитель 2 - в числителе останется 1. а в знаменателе 5. Получается:
1
5*(a+0,4)
ОТМЕТЬ КАК ЛУТШЕЕЕ ТЕБЯ ЭТО ОЧЕНЬ ВАЖНО ТЕБЯ Я ОЧЕНЬ СТАРАЛАСЬ
2с\5а+с\10а=5с/10а=с/2а