Объяснение:
Мы знаем, что помимо положительных чисел, меньше нуля существуют еще и отрицательные числа.
Поэтому, при сложении отрицательного и положительного числа, всегда из положительного числа вычитается отрицательное, то есть, наглядно первый пример можно преобразовать как:
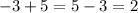, тогда становится понятнее логика сложения отрицательного с положительным числом.
Второй пример аналогичен первому: если из положительного числа, то есть 3, вычесть отрицательное число, то есть 5, получим как раз -2: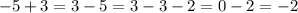 
.
Пойдем ниже, в третьем примере из положительного числа вычитают большее отрицательное число. Поэтому в таких случаях запись можно преобразовать как: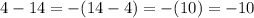 
, то есть, мы из отрицательного числа вычитаем положительное число и заносим эту операцию над двумя числами в скобки со знаком "минус".
Четвертый и пятый пример аналогичны первому, когда мы можем представить запись в виде:
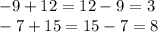
То есть, если число со знаком "+" больше числа со знаком "-", мы имеем право переписать запись в виде обычного вычитания из большего числа меньшее, где получим положительное число в ответе.
Таких примеров можно привести много. Разберём один из них и принцип решения:
Пусть, например первые пять чисел равны 1, 2, 3, 4 и 5, а шестое число равно х (х≠0).
Тогда произведение этих чисел равно 1*2*3*4*5*х
Увеличим каждое из чисел на 1, получим числа: 2, 3, 4, 5, 6 и х+1.
Их произведение равно 2*3*4*5*6*(х+1).
По условию, от увеличения каждого из чисел на единицу, их произведение чисел не изменилось. Составим уравнение:
1*2*3*4*5*х = 2*3*4*5*6*(х+1)
х = 6(х+1)
х = 6х+6
х-6х = 6
-5х = 6
х = -6:5
х = -1,2
1, 2, 3, 4, 5, -1,2