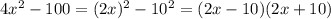
1.
а)а⁴-81;
б)n⁴-72n²+1296;
в)5х²+2у²+11ху.
2)х=11/60.
Объяснение:
1)Представить в виде многочлена:
а)(а²+9)(а+3)(а-3)= разность квадратов (а+3)(а-3), свернуть:
=(а²+9)(а²-9)= разность квадратов (а²+9)(а²-9), свернуть:
=а⁴-81;
б)(n-6)²(n+6)²=
=(n-6)(n-6)(n+6)(n+6)= разность квадратов (n-6)(n+6), свернуть:
=(n²-36)(n²-36)=
=(n²-36)²= квадрат разности, развернуть:
=n⁴-72n²+1296;
в)(у+3х)(3х-у)-(х-3у)(4х+у)= разность квадратов (у+3х)(3х-у), свернуть:
=9х²-у²-(4х²+ху-12ху-3у²)=
=9х²-у²-4х²-ху+12ху+3у²=
=5х²+2у²+11ху.
2)Найти корень уравнения:
12х(3х-5)-(6х-2)(6х+2)= -7 разность квадратов(6х-2)(6х+2), свернуть:
36х²-60х-(36х²-4)= -7
36х²-60х-36х²+4= -7
-60х= -7-4
-60х= -11
х= -11/-60
х=11/60.
ответ:Отметь как лучший ответ
Объяснение:
1) Найти область определения функции;
Ограничений нет - х ∈ R (знаменатель не может быть равен нулю).
2) Исследовать функцию на непрерывность;
Непрерывна, так как нет точек разрыва функции.
3) Определить, является ли данная функция четной, нечетной;
f(-x) = ((-x)-3)²/((-x)² +9) = (x+3)²/(x² +9) ≠ f(-x) ≠ -f(-x).
Функция не чётная и не нечётная.
4) Найти интервалы функции и точки её экстремума ;
Находим производную функции.
y' = 6(x-3)(х+3)/(x² + 9)².
Приравняв её нулю (достаточно только числитель), имеем 2 корня:
х = 3 и х = -3.
Имеем 3 промежутка (-∞; -3), (-3; 3) и (3; ∞).
Находим знаки производной на этих промежутках.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
x = -4 -3 0 3 4
y' = 0,0672 0 -0,66667 0 0,0672.
Отсюда получаем:
Функция возрастает на промежутках (-∞; -3), (3; +∞) и убывает на промежутке (-3; 3)
Экстремумов два:
- максимум в точке х = -3,
- минимум в точке х = 3.
5) Найти интервалы выпуклости и вогнутости и точки перегиба графика функции;
Находим вторую производную.
y'' = -12х(x² - 27)/(x² + 9)³.
Приравняв нулю, имеем 3 точки перегиба:
х = 0, х = √27 = 3√3 и х = -3√3.
6) Найти асимптоты графика функции.
Асимптота есть одна горизонтальная у =1.
График функции, таблица точек для его построения приведены в приложении.