Question

4. В урне находятся 7 белых и 3 черных шара. Подряд извлекают два шара. Какова вероятность того, что они оба черные?

Answer 1

ОТВЕТ: 1/15.

Решение Пусть событие А - оба шара черные.

Воспользуемся классическим определением вероятности. Вероятность события А найдем как отношение числа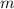 $m$ благоприятных исходов к числу 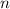$n$ всех возможных исходов: $p(A)=\frac{m}{n}$.

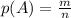Всего шаров 7 + 3 = 10. Выбрать 2 шара из 10 - поскольку не учитывается порядок - можно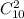 $C_{10}^{2}$ поэтому

$n=C_{10}^{2}=\frac{10!}{2!(10-2)!}=\frac{10\cdot9}{2}=45.$

Выбрать 2 черных шара из 3 можно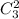 $C_3^2$ поэтому

$m=C_3^2=\frac{3!}{2!(3-2)!} =\frac{3}{1}=3.$

Итого $p(A)=\frac{3}{45}=\frac{1}{15}$

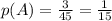
Разобьем событие как бы на два других: В - первый шар будет черным; С - второй шар будет черным.

Вероятность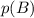 $p(B)$ того, что первый шар будет черным, по определению вероятности равна  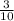$\frac{3}{10}$, поскольку всего шаров 10, а черных - 3. После того, как взяли один черный шар, всего осталось 9 шаров, из которых 2 черных. Поэтому вероятность 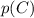$p(C)$ того, что второй шар будет черный, равна $\frac{2}{9}$.

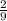Поскольку необходимо, чтобы одновременно и первый, и второй шар были черными, искомую вероятность можно найти, перемножив вероятности событий В и С, т.е. $p(A) = p(B)\cdot p(C)=\frac{3}{10}\cdot\frac{2}{9}=\frac{1}{15}.$