Объяснение:
1) Приведения обеих частей уравнения к одному основанию.
2) Разложение на множители.
3) Введение новой переменной.
4) Логарифмирование обеих частей (о нем разговор позже).
5) Искусственные приемы.
Из предложенных уравнений выбрать те, которые соответствуют обозначенным решения (устно):
1) 5х + 1 = 125 2) 43 – 2х = 22(х - 1)
3) 2х + 2х + 1 = 12 4) 5х – 2 – 5х – 1 + 5х = 21
5) 2 * 9х – 3х + 1 – 9 = 0 6) 25х – 26 * 5х + 25 = 0
(далее предложить эти уравнения для домашней работы).
II. Решение показательных уравнений (работа в группах).
В зависимости от состава групп уровень сложности уравнений нарастает. Каждая группа решает по 3 уравнения, потом представляет свое решение (отчитывается о проделанной работе).
Две слабые группы работают с листами самопроверки, на которых предложен ход решения заданий. Остальным группам предложить карточки с ответами, которые они должны получить.
I, II группы (слабые)
1. 32х + 1 = 92х
2. 7х + 2 – 7х = 336
3. 2 * 22х – 3 * 2х – 2 = 0
Дополнительное уравнение: 9х – 3х – 6 = 0
III группа (средние)
1. 2х2 – 6х + 0,5 = 1__
16√2
2. 4х – 1 + 4х + 4х + 1 = 84
3. 34√х – 4 * 32√х + 3 = 0
IV, V группы (сильные)
1. 4 (√(3х2 – 2х)) + 1 + 2 = 9 *2√(3х2 – 2х)
2. 3 * 16х + 2 * 81х = 5 * 36х
3. 52х – 1 + 22х = 52х – 22х + 2
III. Искусственный прием решения показательных уравнений (разобрать у доски).
1) (4 + √15)х + (4 - √15)х = 8
Числа 4 + √15 и 4 - √15 являются сопряженными.
Действительно (4 + √15)(4 - √15) = 16 – 15 = 1.
Поэтому 4 - √15 = 1
4 + √15
Введем новую переменную (4 + √15)х = t > 0
Получим: t + 1/t = 8
t2 – 8t + 1 = 0
t1 = 4 + √15; t2 = 4 - √15
(4 + √15)х = 4 + √15; (4 + √15)х = 4 - √15
x = 1 (4 + √15)х = 1
4 + √15
(4 + √15)х = (4 + √15)-1
x = -1
2) Пробуют по аналогии решить самостоятельно (на обороте доски – решение для проверки).
(2 + √3)х + (2 - √3)х = 4
IV. Решение систем показательных уравнений.
1. Метод приведения к одному основанию.
1) 82х + 1 = 32 * 24у – 1
{
5 * 5х-у = √252у + 1
2) 3х * 9у = 3
{
2у - х = 1
2х 64
2. Метод введения новых переменных.
1) х + 5у + 2 = 9 5 у+2 = t
{
2х – 5у + 3 = 11
2) 3 * 7х – 3у = 12 7x = a
{
7х * 3у = 15 3y = b
Итог урока: Обобщить различные решения показательных уравнений и систем уравнений.
Домашнее задание (дифференцированное, выборка из сборников тестов подготовки к ЕНТ).
«-» 1) 5х + 1 = 125
2) 43 – 2х = 22(х - 1)
3) 2х + 2х +1 = 12
4) 5х – 2 – 5х – 1 + 5х = 21
5) 2 * 9х – 3х + 1 - 9 =0
6) 25х – 26 * 5х + 25 = 0
«+» 1) 2х + 2 - 2х + 3 – 2х+ 4 = 5х + 1 – 5х + 2
2) (√(6 – х)) (5х2 – 7,2х + 3,4 - 25) = 0
3) 2 * 25х – 5 * 10х + 2 * 4х = 0
4) 5(sinx)2 – 25cosx = 0
5) 2 * 4х + 3 * 5у = 11
{
5 * 4х + 4 *5у = 24
6) 27х = 9у
{
81х : 3у = 243


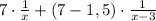
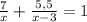

Если я правильно понял Вашу запись, то восьмой член прогрессии равен 2.56, а q равен 2. Приступим. b8=b1*q^7 => b1=b8/q^7. b1=0.01. Может решения мой не самый удобный, но что-то тянет действовать "в лоб" и тупо найти сумму.
получается
сумма первых восьми членов равна = b1 + b1*2 + b1*4 + b1*8 + b1 * 16 + b1 * 32 + b1*64 + b1 * 128 + b1* 256 = b1 (1+2+4+8+16+32+64+128+256) = 0.01 * 511= 5.11.
ответ: сумма первых восьми членов геометрической прогрессии равна 5.11.