Эту задачу можно решить с системы уравнения:
Пусть х будет ЧАСЫ, за которые первый печник сделает работу отдельно
Пусть у будет ЧАСЫ, за которые второй печник сделает работу отдельно
Теперь узнаем сколько оба печника сделают работу за 1 час:
Получаем:
1/х- сделает первый печник за 1 час
1/у- сделает второй печник за 1 час
Тогда нужно решить эту систему из 2-х уравнений
Получаем:
1/Х+1/У =1/12 и 2/Х +3/У = 1/5 (20%- 1/5 задания)
Каждое слагаемое 1-ого уравнения мы умнажаем на 2 и вычтем его из 2-ого уравнения.
Из этого мы получаем:
1/У =1/5 - 1/6 = 1/30, тогда У=30; следовательно 1/Х =1/12 -1/30 = 3/60 =1/20 тогда Х=20
ответ: Первый печник будет работать 20 часов; а второй будет работать 30 часов
Пусть первый пешеход движется со скоростью x км/ч, а второй - y км/ч.
В первом случае первый пешеход будет двигаться до встречи 4,5 ч , в то время как второй 2,5 ч (так как он вышел на два часа раньше второго). Из этого получаем уравнение: 4,5x+2,5y=30
Во втором случае второй пешеход шел 5 ч, а первый пешеход шел 5-2=3ч. Получаем второе уравнение: 3x+5y=30
Из этих двух уравнений составляем систему

Умножеим первое уравнение системы на 2:
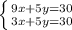
Вычтем из первого уравнения второе, получим:
6x=30
x=30:6
x=5.
Подставляя во второе уравнение, находим
3*5+5y=30
15+5y=30
5y=15
y=3
ответ: скорость первого - 5 км/ч, скорость второго - 3 км/ч.
Объяснение:
В итоге - выполнен весь объем работ.
7 * 1/Х + 8 * (1/Х + 1/(Х + 7)) = 1.
15/Х + 8/(Х + 7) = 1.
15 * Х + 105 + 8 * Х = Х * Х + 7 * Х.
Х * Х -16 * Х - 105 = 0.
Дискриминант D = 16 * 16 + 4 * 105 = 256 + 420 = 676 = 26 * 26.
Х = (16 + 26) / 2 = 42 / 2 = 21 час - время первой.
21 + 7 = 28 часов - второй.
ответ: Машинистки перепечатают рукопись за 21 час и 28 часов.