применим метод прямоугольного треугольника. Сейчас я опишу его действие. Он позволяет вычислять точныее значения нетабличных углов. Построим прямоугольный треугольник. Пусть у нас угол α будет при стороне b. Пусть arccos 2/3 = α, тогда по определению арккосинуса cos α = 2/3. Видно, что нам надо найти tg 2α. Применим формулу тангенса двойного угла:
tg 2α = 2tg α / 1 - tg² a.
Отсюда следует, что нам нужно найти tga. tg α = sin α/cosα. Косинус мы знаем, надо найти синус.
cos α = b / c
b / c = 2/3
b = 2, c = 3
sin α = a / c
a = √(c² - b²) = √5
Отсюда sin α = √5 / 3
tg α = sin α / cosα = √5/3 : 2/3 = √5/2
Теперь осталось найти всего лишь tg 2α:
tg 2α = √5 / 1 - 5/4 = √5 : -1/4 = -4√5
Таким образом, tg 2α = tg(2arccos 2/3) = -4√5
ответ получен. Всё остальное делаем по аналогии. Рисунок сейчас приложу моих рассуждений
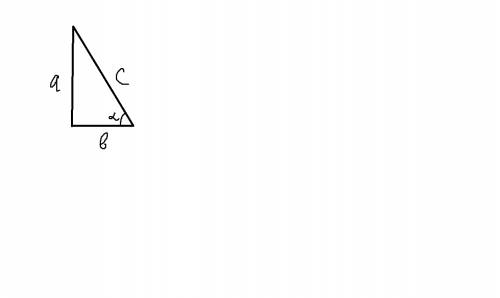
Рассмотрим числовую последовательность в которой члены - это количество камешков в каждом уголке, т.е.
а1=1
а2=3=1+2=а1+2
а3=5=3+2=а2+2
а4=7=5+2=а3+2
Замечаем, что данные числа образуют арифметическую прогрессию с разность d=2 (каждый следующий член получен из предыдущего увеличением на одно и тоже число - 2).
По формуле n-го члена арифметической прогрессии
аn=а1+(n-1)*d
находим, что а100=1+(100-1)*2=1+99*2=1+198=199, т.е. в сотом уголке - 199 камешков.
А, теперь, используя формулу для нахождения суммы первых n членов арифметической прогрессии
Sn=((a1+an)*n)/2
получаем, что в первых 100 уголках будет камешков
S100=((1+199)*100)/2=(200*100)/2=100*100=10000
ответ: 10000