246420
в начале 200000 умножаются на 11% получается 222000 , а потом 222000 умножаются на 10% получается 246420
,
, a 
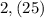
целая часть. У нас она равна 2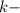
- количество цифр в периоде. У нас их 2
количество цифр до периода. У нас их 0
все цифры, включая период, в виде натурального числа. У нас это 25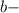
все цифры без периода в виде натурального числа. Их нет.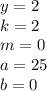
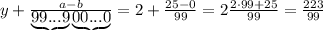
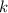подставляется количество 9, а под 
-количество нулей. У нас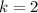 
, значит пишем две цифры 9, а 
, значит, нулей не пишем вообще. Между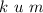 
не стоит знак умножения
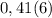
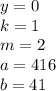
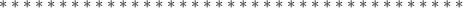
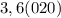
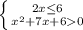
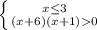
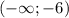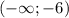и 
и ![(-1;3]](/tpl/images/0188/5648/df8ed.png)
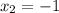
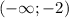и 
![(-4;-2]](/tpl/images/0188/5648/eac16.png)
ответ:1) 200 000 * 11% = 22000
2) 22000 + 200 000 = 222000(после первого года)
3) 222000 * 11% = 24420
4) 222 000 + 24420 = 246420
Объяснение:
ответ 246420