12x^2-4x-1=0
12x^2+2x-6x-1=0
(6x+1)(2×-1)=0
6x+1=0 або 2x-1=0
x=-1/6 x=1/2
В-дь:x=-1/6; x=1/2.
Радиус проведённый в точку касания перпендикулярен касательной.
В четырёхугольнике сумма углов равна 360°.
В четырёхугольнике EOFC:
∠ECF = 360°-∠EOF-∠CEO-∠CFO = 360°-102°-90°-90° = 78°.
В треугольнике сумма углов равна 180°.
В ΔABC:
∠BAC = 180°-∠ABC-∠BCA = 180°-90°-78° = 12°
В четырёхугольнике BEOD:
∠EOD = 360°-∠ODB-∠DBE-∠BEO = 360°-90°-90°-90° = 90°
В четырёхугольнике DOFA:
∠DOF = 360°-∠OFA-∠FAD-∠ADO = 360°-90°-12°-90° = 168°
ответ: ∠A=12°, ∠C=78°, ∠EOD=90° и ∠FOD=168°.
Объяснение:
Не знаю, может и не правильно.
1) 2x - 3y = 6
Точки пересечения с осью Ох: принимаем у=0
2x - 3*0 = 6
2x = 6
x = 3
(3;0) - точка пересечения с осью Ох
Точки пересечения с осью Оу: принимаем х=0
2*0 - 3у = 6
-3у = 6
у = -2
(0;-2) - точка пересечения с осью Оу.
2) x² + y = 4
Точки пересечения с осью Ох: принимаем у=0
x² + 0 = 4
x² = 4
x = ± 2
(-2;0), (2;0) - точки пересечения с осью абсцисс.
Точки пересечения с осью Оу: принимаем х=0
0² + у = 4
у = 4
(0;4) - точка пересечения с осью ординат.
3) |x| + |y| = 7
Точки пересечения с осью Ох: принимаем у = 0.
|x| + |0| = 7
|x| = 7
x = ± 7
(-7;0), (7;0) - точки пересечения с осью абсцисс.
Точки пересечения с осью Оу: принимаем х = 0.
|0| + |y| = 7
|y| = 7
y = ± 7
(0;-7), (0;7) - точки пересечения с осью ординат.
Объяснение:
1x =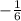
2x = 0,5
P.s. Это не два x, это первый и второй x
Объяснение:
В данном случаи есть два решения квадратного уравнения, но я решу через один
1) Через дискриминант:
1) D =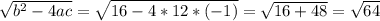
x =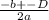
(для каждого x свой знак, либо + либо -) (для какого x какой знак выбираешь сам)
1x =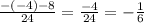
2x =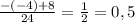
Это корни уравнения (в квадратном их всегда два)