Разобьем числа от 1000 до 9999 на следующие группы:
от 1000 до 1999, от 2000 до 2999, ..., от 9000 до 9999.
В каждой группе, очевидно, на первом месте стоит ненулевая цифра, поэтому их можно без каких-либо проблем отбросить. Отбросив их все, мы получим 9 совершенно одинаковых групп вида:
000, 001, 002, ..., 999.
Найдем количество нулей в одной такой группе.
Заметим, что эта группа представляет собой набор всевозможных упорядоченных последовательностей из трех цифр. Таким образом, можно сделать вывод, что каждая цифра в этом наборе написана одинаковое количество раз.
Всего в группе 000, 001, 002, ..., 999 имеется 1000 последовательностей, соответственно для их записи использовано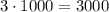 
цифр. Значит, каждая из десяти цифр записана по 
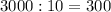раз.
Итак, цифра 0, как и любая другая цифра встречается в одной группе 300 раз. Значит, в девяти таких группах она встречается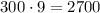 
раз.
ответ: 2700
1) x²-3-4<0;(х-√7)(х+√7)<0;
-√7√7
+ - +
х∈(-√7;√7)
второе решение на случай, если при втором коэффициенте потерян х. x²-3х-4<0; по Виету корни левой части -1 и 4.
-14
+ - +
х∈(-1;4)
2) x²-3x-4>0 уже решил. как второй вариант первого. только здесь другой знак. поэтому ответ х∈(-∞;-2.5)∪(1;+∞)
Решение
x²-3х-4>0; по Виету корни левой части -1 и 4.
-14
+ - +
ответ х∈(-∞;-2.5)∪(1;+∞)
3) 2x²+3x-5>0 , по Виету корни левой части 1 и -2.5
-2.51
+ - +
х∈(-∞;-2.5)∪(1;+∞)
4) -6x²+6x+36>0
-6*(x²-x-6)>0; (x²-x-6)<0;
По Виету x=-2; x=3.
-23
+ - +
х∈(-2;3)
92-20=76(км/ч)
76:2=38(км/ч)