1)Решение системы уравнений х=2
у=3
2)Решение системы уравнений х= -3,5
у= -3
3)Решение системы уравнений х=2
у=1
Объяснение:
Решить системы уравнений методом подстановки:
1)2х-у=1
7х-6у= -4
Выразим у через х в первом уравнении, подставим выражение во второе уравнение и вычислим х:
-у=1-2х
у=2х-1
7х-6(2х-1)= -4
7х-12х+6= -4
-5х= -4-6
-5х= -10
х= -10/-5
х=2
у=2х-1
у=2*2-1=3
у=3
Решение системы уравнений х=2
у=3
2)2х-3у=2
4х-5у=1
Разделим первое уравнение на 2 для удобства вычислений:
х-1,5у=1
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х=1+1,5у
4(1+1,5у)-5у=1
4+6у-5у=1
у=1-4
у= -3
х=1+1,5у
х=1+1,5*(-3)=1-4,5
х= -3,5
Решение системы уравнений х= -3,5
у= -3
3)2(х+2у)-3(х-у)=5
4(х+3у)-3у=17
Раскроем скобки, приведём подобные члены:
2х+4у-3х+3у=5
4х+12у-3у=17
-х+7у=5
4х+9у=17
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
-х=5-7у
х=7у-5
4(7у-5)+9у=17
28у-20+9у=17
37у=17+20
37у=37
у=1
х=7у-5
х=7*1-5
х=2
Решение системы уравнений х=2
у=1
Если 2 стула дороже, чем один стол на 100 грн., то 4 стула дороже, чем два стола на 200 грн.
Пусть стол стоит х грн., тогда 3 стола стоят 3х грн., а 4 стула заменим двумя столами и 200 гривнами, тогда стоимость покупки из 3 столов и 4 стульев будет такой
3*х+(2*х+200)=4700
5х=4700-200
5х=4500
х=900, значит, один стол стоит 900 грн., тогда если к этой сумме добавить 100 грн. и разделить на два, получим цену стула, т.е. (900+100)/2=500
Значит, 500 грн. стоит стул.
традиционный.
цена стола х, цена стула у, отсюда система уравнений
2у-х=100
3х+4у=4700
Первое уравнение умножим на 3 и сложим со вторым. Получим
-3х+6у=300
3х+4у=4700
10у=5000, откуда у=5000/10
у=500, стул стоит 500 грн. , тогда стол стоит х=2у-100=2*500-100=900
Стол стоит 900 грн.
1) c² + b³ - cb + c - cb² - b² = (c² - cb + c) + (b³ - cb² - b²) =
= c(c - b + 1) + b²(b - c - 1) = c(c - b + 1) - b²( c - b + 1) = (c - b + 1)(c - b²)
2) (x + y - 7)² + (x - 2y + 2)² = 0
Это равенство верно только в случае, когда :
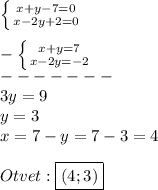
3) Пусть надо взять х кг 25% - го и y кг 50% - го сплавов меди . Надо получить 20 кг 40% - го сплава.
x y 20 = x + y
25% 50% 40%
0,25x + 0,5y = 0,4(x + y)
Если x + y = 20 , то y = 20 - x
0,25x + 0,5 * (20 - x) = 0,4 * 20
0,25x + 10 - 0,5x = 8
- 0,25x = - 2
x = 8 кг - 25% - го
y = 20 - 8 = 12 кг - 50% - го
ответ : надо взять 8 кг 25% - го и 12 кг 50% - го сплавов
вот ответ с методом подстановки