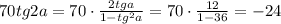
вот так
Объяснение:
1. Определи угол между диагоналями, которые находятся в соседних гранях куба и имеют общий конец:
image
Так как куб — правильный многогранник, в независимости от размещения данных диагоналей, достаточно рассмотерть такой треугольник, который образован из двух данных диагоналей и еще одной, которая соединяет концы данных диагоналей.
У куба все грани — равные квадраты, диагонали которых одинаковы. Треугольник равносторонний, и угол между DC1 и DB равен 60°.
2. Определи угол между диагоналями, которые находятся в соседних гранях куба и не имеют общий конец:
image
Так как куб — правильный многогранник, в независимости от размещения данных диагоналей, достаточно рассмотерть диагонали 1 и 2. Они скрещивающиеся, поэтому переместим их в одну плоскость, передевигая диагональ 2 на 3.
Получилась уже рассмотренная ситуация, и угол между BD и AD1 равен 60°.
3. Определи угол между диагоналями, которые находятся в противоположных гранях куба, но не параллельны:
image
Так как куб — правильный многогранник, в независимости от размещения данных диагоналей, достаточно рассмотерть диагонали 1 и 2. Они скрещивающиеся, поэтому переместим их в одну плоскость, передевигая диагональ 2 на 3.
У куба все грани — квадраты, диагонали квадрата перпендикулярны, и угол между DA1 и BC1 равен 90°.
-2 и 2 или 2,8 и 0,4.
Объяснение:
Пусть х и у - данные числа. По условию
х^2 + у^2 = 8 и (х + 2) + (3у) = 6.
Составим и решим систему уравнений:
{х^2 + у^2 = 8,
{х + 2 + 3у = 6;
{х^2 + у^2 = 8,
{х = 4-3у;
{(4-3у)^2 + у^2 = 8,
{х = 4-3у;
Решим отдельно первое уравнение:
(4-3у)^2 + у^2 = 8
16+9у^2-24у+у^2-8=0
10у^2 - 24у + 8 = 0
5у^2 - 12у + 4 = 0
D = 144 - 80 = 64;
y1 = (12+8)/10 = 2;
y2 = (12-8)/10 = 0,4.
Если второе число у=2, то первое равно х = 4-3у = 4 - 3•2 = -2;
Если второе число у=0,4, то первое равно х = 4-3у = 4 - 3•0,4 = 4 - 1,2 = 2,8.
ответ: -2 и 2 или 2,8 и 0,4.
Проверим полученный результат:
1. (-2)^2 + 2^2 = 8 и (-2 + 2) + (3•2) = 6 - верно.
2. 2,8^2 + 0,4^2 = 8 и (2,8 + 2) + (3•0,4) = 6 - верно.