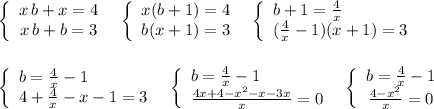
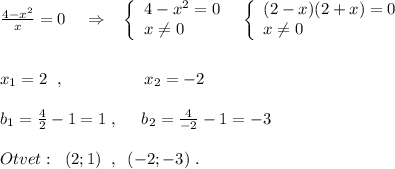
ответ: за 5 ч.
Объяснение:
Пусть V - объём бассейна. Пусть V1 - объём воды, который поступает в бассейн за 1 час из одной трубы, а V2 - объём воды, который поступает в бассейн за 1 час из крана. Тогда (так как по условию трубы одинаковы) отсюда следуют уравнения 8*V1+V2=V и 6*V1+2*V2=V. Получена система уравнений:
8*V1+V2=V
6*V1+2*V2=V.
Умножив первое уравнение на 3, а второе - на 4, перепишем эту систему так:
24*V1+3*V2=3*V
24*V1+8*V2=4*V.
Вычитая из второго уравнения первое, получим уравнение 5*V2=V. Отсюда V2=1/5*V, то есть за 1 час кран наполняет 1/5 часть бассейна. Значит, весь бассейн кран наполнит за время t=V/V2=5 ч.
Скорость автомобиля 70 км/ч, автобуса 60 км/ч
Объяснение:
Пусть скорость автомобиля Х, а автобуса У
Раз после того, как из одной исходной скорости вычли 10, а к другой прибавили 10, автобус и автомобиль "поменялись местами" (до этого автомобиль приезжал на час быстрее, а потом автобус стал приезжать на час быстрее), то (Х-У)=10
У=Х-10
Составляем уравнение
420/Х=420/(Х-10)-1
420*(Х-10)/Х=420-Х+10
420Х-4200=430Х-Х^2
Х^2-10X-4200=0
По теореме Виета х1=70 х2=-60.
Положительный корень один х=70.
Скорость автомобиля 70 км/ч, автобуса 60 км/ч
Другое решение:
420/Х=420/У-1
Отсюда ХУ=420*(Х-У)
Второе уравнение
420/(Х-10)=420/(У+10)+1
Отсюда 420(У+10)=420*(Х-10)+(Х-10)*(У+10)
420(У-Х)=-8500+ХУ+10(Х-У)
8500-430(Х-У)=ХУ
Приравниваем
8500-430(Х-У)=420(Х-У)
8500=850*(Х-У)
Х-У=10
Дальше также:
420/Х=420/(Х-10)-1
420*(Х-10)/Х=420-Х+10
420Х-4200=430Х-Х^2
Х^2-10X-4200=0
По теореме Виета х1=70 х2=-60.
Положительный корень один х=70.
Первый изящнее, но не очевидно, что решение единственно.
Второй в этом смысле корректнее.