Объяснение:
-х2 ‹ -2,7х
-х2 +2,7х‹0
х2-2,7х>0
х(х-2,7)>0
х>0 х-2,7>0
х>2,7
ответ:х>0; х>2,7
В решении.
Объяснение:
а) (х + 7)(х - 1) >= 0
В левой части неравенства квадратное уравнение, в котором
х₁ = -7, х₂ = 1.
График квадратичной функции - парабола.
Значения х - это точки пересечения параболой оси Ох, ветви вверх.
Представить эту параболу мысленно, или набросать схематично (ничего вычислять не нужно) и посмотреть, при каких значениях х парабола выше оси Ох (у >= 0, как в неравенстве).
Решение неравенства: х∈(-∞; -7]∪[1; +∞), объединение.
б) (х - 3)(х - 5) <= 0
Методика та же, что в предыдущем решении, только смотреть параболу ниже оси Ох:
х₁ = 3; х₂ = 5.
Решение неравенства: х∈[3; 5], пересечение.
в) (х - 2)(х + 3) < 0
х₁ = 2; х₂ = -3.
Решение неравенства: х∈(-3; 2), пересечение.
г) (а + 2)(а - 5) <= 0
а₁ = -2; а₂ = 5.
Решение неравенства: х∈[-2; 5], пересечение.
г) (t + 3)(t + 4) >= 0
t₁ = -3; t₂ = -4.
Решение неравенства: х∈(-∞; -4]∪[-3; +∞), объединение.
д) (2 - с)(3 - с) >= 0
-(c - 2) * -(c - 3) >= 0
(c - 2)(c - 3) >= 0
c₁ = 2; c₂ = 3
Решение неравенства: х∈(-∞; 2]∪[3; +∞), объединение.
Примечание: если знак >= или <=, неравенство нестрогое, скобка квадратная при числах. Знаки бесконечности всегда с круглой скобкой.
Если знак > или <, неравенство строгое, скобка круглая.
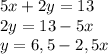
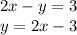
2х^2+х+7=-х^2+5х+(-2-х^2)
-2х^2+х+7= -х^2+5х-2-х^2
-2х^2+х+7=-2х^2+5х-2
-2х^2+х+7+2х^2-5х+2=0
-4х+9=0
-4х=-9
х=-9/-4
х=2,25
ответ:2,25
Объяснение: