F(5)=5 f(-2)=-2 f(0)=0 если понравился ответ в берите в качестве лучшего
- это парабола, ветви которой направлены вверх. Соответственно, если вершина этой параболы будет лежать в области определения функции y (т.е. будет выше оси абсцисс), то именно в ней достигается наименьшее значение. Если у этой параболы есть корни, то наименьшее значение функции будет равно нулю (т.к. выражение под корнем не может быть меньше нуля). Дабы убедиться, что корней нет, проверим дискриминант: 
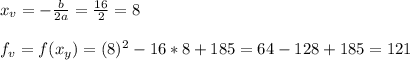
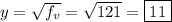
f(5) = 5
f(-2) = -2
f(0) = 0
Объяснение:
f(5) = 5
f(-2) = -2
f(0) = 0
f(x) также можно представить как y