Даана параллельная прямая а и б,точка А на одной из прямых и отрезок н.Найди точку на другой прямой на расстояние ,равном длине данного отрезка н от данной точки А
У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Букв у нас 10, 3 буквы А, по 2 буквы М и Т, и по одной Е, И и К. На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10! Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы. Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами. Для М и Т это будет 2! и 2!, для А – 3! С учётом порядка позиции их будет: Тогда вероятность (согласно классическому определению):
Попробуем другой, более простой Перестановки с повторением. Всего у нас Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность:
Правильное условие такое:
У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок?
Решение.
ОДЗ: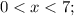

Методом подбора быстрее.
1) Начнем с решения второго уравнения.
Если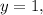 то 7-1=6. Тогда
то 7-1=6. Тогда  не натуральное число.
не натуральное число.
Если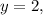 то 7-2=5. Тогда
то 7-2=5. Тогда 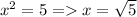 не натуральное число.
не натуральное число.
Если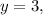 то 7-3=4. Тогда
то 7-3=4. Тогда 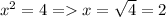 натуральное число.
натуральное число.
Получили решение
2) Подставим
 в первое уравнение
в первое уравнение  .
.
ответ: 2 груши у брата;
3 яблока у сестры.