S=108
Объяснение:
d=15
a=b+3
Через теорему Пифагора находим одну из сторон:
c^2 = a^2 + b^2
c^2 = (b+3)^2 + b^2
225= 2b^2 + 6b + 9
Получаем квадратное уравнение и решаем его:
2b^2 + 6b - 216=0 (/2)-сокращаем на 2
b^2 + 3b - 108=0
Сразу ставим условие что b>0 (не может же сторона быть отрицательной длинны)
D=9+432=441 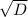 =21
=21
b1= 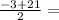 9
9
b2= 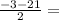 -12 (не удв. решению)
-12 (не удв. решению)
b=9
Подставляем b:
a = b-3
a=9+3
a=12
Далее подставляем значения в формулу площади прямоугольника:
S=a*b
S=9*12
S=108
Кол-во таких чисел=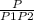 .
.
Здесь P -общее кол0во перестановок 6 чисел : P=6!=60*12
P1 - число перестановок цифры 1 в этом числе. То есть мы как бы путем деления общего числа перестановок на число перестановк конкретной цифры убираем повторяющиеся перестановки, образуемые этой цифрой. Так как кол-во единиц в наборе 2 штуки, то
P1=2!=2
Аналогично для P2=3!=6
P= 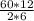 =60.
=60.
если бы например в наборе были бы только единицы напрмиер, то получилось бы единственное возможное число, что доказывает некоторую универсальность моей формулой
108 см²
Объяснение:
С т.Пифагора:
Пусть x см- 1 сторона, тогда 2 сторона=(x+3)см. Известно, что диагональ 15 см. Составим и решим уравнение:
x²+(x+3)²=15²;
x²+x²+6x+9=15²;
2x²+6x+9-225=0;
2x²+6x-216=0;
D=36-4×2×(-216)=36+1728=1764;
x1,2=-6±42/4;
x1=9;
x2=-12 - не удовл. усл. x>0
Значит, 9 см- 1 сторона
9+3=12 (см) - другая сторона
S= 12×9=108 см²