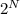(это если учитывать пустое множество и само множество). Доказать это можно с метода математической индукции. Формула очевидна для маленьких N. Например, если в множестве один элемент, то подмножеств два - пустое и само множество. Пусть для N-элементного множества число подмножеств равно 
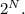Добавим еще один элемент. Все подмножества нового множества разбиваются на две категории - те, которые не содержат новый элемент (их по предположению 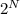штук) и те, которые его содержат (их тоже 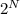штук, так как они могут быть получены из подмножеств первого типа добавлением нового элемента). Всего получаем
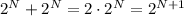подмножеств, что и требовалось доказать.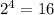 
1)
3,81*106 л = 403,86 л
1 л = 1 дм³
1 м³ = 1000 дм³
403,86 л = 403,86 дм³ = 0,40386 м³
0,40386 м³ = 4,0386 * 10⁻¹ м³
2)
54*105 км/ч = 5670 км/ч
1 км = 1000м
1 ч = 3600 с
5670 км/ч = (5670*1000 м)/3600 с = 1575 м/с
1575 м/с = 1,575 * 10³ м/с
3)
2,3*108 м² = 248,4 м²
1 га = 10000 м²
248,4 м² = 0,02484 га
0,02484 га = 2,484*10⁻² га
4)
3,21*106 л = 340,26 л
1 л = 1 дм³
1 м³ = 1000 дм³
340,26 л = 340,26 дм³ = 0,34026 м³
0,34026 м³ = 3,4026 * 10⁻¹ м³
5)
72*103 км/ч = 7416 км/ч
1 км = 1000м
1 ч = 3600 с
7416 км/ч = (7416*1000 м)/3600 с = 2060 м/с
2060 м/с = 2,06 * 10³ м/с
6)
2,2*106 м² = 233,2 м²
1 га = 10000 м²
233,2 м² = 0,02332 га
0,02332 га = 2,332*10⁻² га