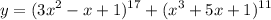
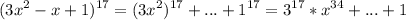
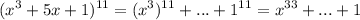
Уточнение : десятичная периодическая дробь, как и конечная десятичная дробь, являются рациональными числами. Записать периодическую дробь можно в виде смешанного числа, либо в виде обыкновенной дроби, если целая часть равна нулю.
Чтобы записать периодическую дробь в виде смешанного числа, нужно оставить целую часть без изменения, а дробную часть периодической дроби, у которой период начинается сразу после запятой, записать в виде обыкновенной дроби, в которой числитель - это число из периода, а знаменатель содержит столько девяток, сколько цифр в периоде.
А) 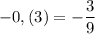
Б) 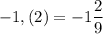
В) 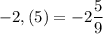
Г) 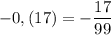
Д) 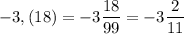
Е) 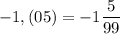
Если период равен нулю, то его можно просто отбросить, оставив число до периода : целое либо в виде конечной десятичной дроби.
Ж) 2,(0) = 2
З) -0,(0) = 0
И) 4,37(0) = 4,37
1)x^2 + 7x = 0
x(x+7) = 0
x = 0 и x + 7 = 0
x = -7
2)12x^2 - 5x - 2 = 0
D= b^2 - 4ac = 5^2 - ( -4 *(12 * 2)) = 121
x1,2 = -5 +- корень 122\24
Возможные решение :
- 2\3
1\4
3)x^2 - 6x + 9 = 0
D = (-6)^2 - 4 * 1 * 9 = 36 - 36 = 0
D = 0 , 1 корень
x = -b\2a
x = 6\2 = 3
4)x^2 - 3x + 11 = 0
D = 3 * 3 - 11 * 4 = 35
D<0 нет корней
Объяснение: