Х² + 9х = 0
I.Рациональный решения.
Вынести общий множитель за скобку:
х * (х + 9 ) = 0
Произведение = 0 , если один из множителей =0.
х₁= 0
х + 9=0
х₂= -9
II. Решение через дискриминант [ D= b² -4ac ]
Стандартный вид квадратного уравнения:
х² + 9х + 0 =0
а = 1 ; b= 9 ; с = 0
D = 9² - 4*1*0 = 9²
D>0 - два корня уравнения [ х₁,₂ = (-b ⁺₋ √D)/2a ) ]
х₁ = ( - 9 + √9²) /(2*1) = (-9 + 9)/2 = 0/2 = 0
x₂ = ( - 9 - √9²) /(2*1) = (-9 - 9)/2 = -18/2 = - 9
ответ: ( - 9 ; 0 ) .
Объяснение:
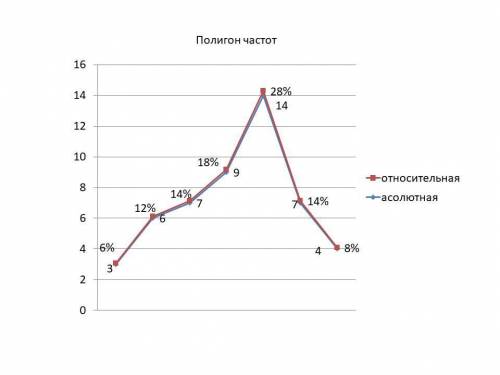
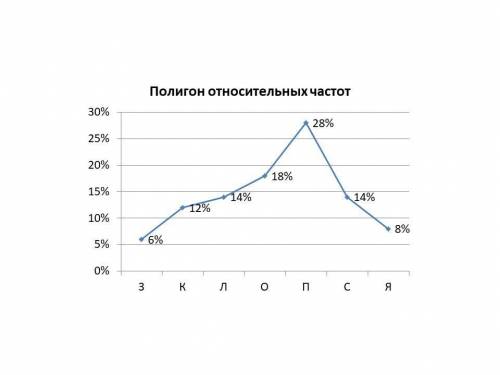
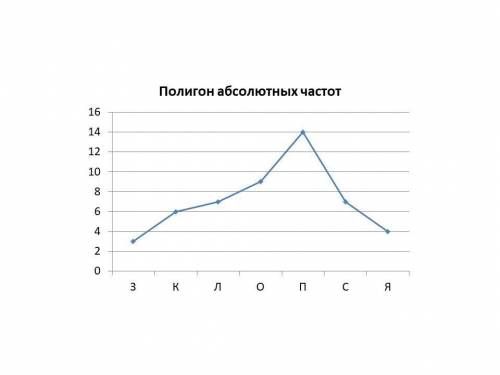
a) Представьте эти данные в виде таблицы абсолютной и относительной частот.
Абсолютные частоты Относительные частоты
З- 3 3 : 50 х100% = 6%
К-6 6 : 50 х100% = 12%
Л-7 7 : 50 х100% = 14%
О -9 9 : 50 х100% = 18%
П-14 14 : 50 х100% = 28%
С -7 7 : 50 х100% = 14%
Я-4 4 : 50 х100% = 8%
b) Проверьте данные таблицы на непротиворечивость.
6% +12%+14% +18%+28%+14%+8% =100%
Противоречий нет
с) Представьте полигон частот ( прицеплены файлом)
Объяснение:
Объяснение:
Функция задана формулой y= -3x+1
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у 4 1 -2
Определите:
1) значение функции, если значение аргумента равно 4;
Чтобы найти значение у, нужно известное значение х подставить в уравнение и вычислить у:
х=4
у= -3*4+1= -11 при х=4 у= -11
2)значения аргумента , при котором значение функции равно -5
Чтобы найти значение х, нужно известное значение у подставить в уравнение и вычислить х:
у= -5
-5= -3х+1
3х=1+5
3х=6
х=2 у= -5 при х=2
3)проходит ли график функции через точку А(-2;7)
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
A (−2; 7)
y = −3x + 1
7= -3*(-2)+1
7=6+1
7=7, проходит.