 ;
;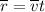 ;
;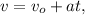 либо в векторном виде:
либо в векторном виде: 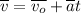 ;
;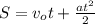 либо в векторном виде:
либо в векторном виде: 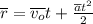 ;
;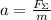 либо в векторном виде:
либо в векторном виде: 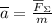 ;
; ;
;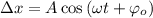 ;
;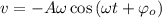 ;
; ;
;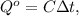 где
где 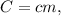 либо в удельном виде:
либо в удельном виде:  ;
;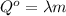 ;
;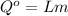 ;
; ;
; ;
;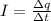 ;
;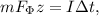 где
где  ;
;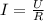 ;
;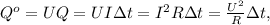
 ;
;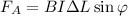 ;
; ;
;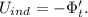
cos(3x+3y) = cos((2x+y) + (2y+x)) = cos(2x+y)*cos(2y+x) - sin(2x+y)*sin(2y+x)
Обозначим 2x+y = a; 2y+x = b.
Нам надо найти:
cos a*cos b - sin a*sin b
Нам известно:
{ cos a - cos b = 1/2
{ sin a - sin b = 1
Возводим в квадрат оба уравнения
{ (cos a - cos b)^2 = cos^2 a - 2cos a*cos b + cos^2 b = 1/4
{ (sin a - sin b)^2 = sin^2 a - 2sin a*sin b + sin^2 b = 1
Складываем уравнения
cos^2 a + sin^2 a - 2(cos a*cos b + sin a*sin b) + cos^2 b + sin^2 a = 5/4
1 - 2cos(a-b) + 1 = 5/4
cos(a-b) = 2 - 5/4 = 3/4
ответ: 3/4
1) График функции обращен выпуклостью вверх, если вторая производная отрицательная: Y"(x)<0 .
Y'(x)=(x^3/(x^2+12))'= ( (x^3)' * (x^2+12)- (x^2+12)' * (x^3) ) /(x^2+12) ^2 =
= (3*x^2*( x^2+12) -2*x*x^3) /(x^2+12) ^2 = (3*x^4+36 *x^2 -2*x^4) /(x^2+12) ^2=
= (x^4+36 *x^2 ) /(x^2+12) ^2 .
Y"(x) = ( (x^4+36 *x^2 ) /(x^2+12) ^2 )' = (x^4+36 *x^2 )' * (x^2+12) ^2 - ((x^2+12) ^2 )' *(x^4+36 *x^2 ) /(x^2+12) ^4 = (4*x^3+72*x)*(x^4+24*x^2+144)-2* (x^2+12)*2*x *
* (x^4+36 *x^2 ) /(x^2+12) ^4= (4*x^7+96*x^5+144*4*x^3+72*x^5+72*24*x^3+72*144*x-(4*x^3+48*x)* (x^4+36 *x^2 ) /(x^2+12) ^4=... упростить многочлен в числителе и решить неравенство Y"(x)<0 ,
Простите, что не довела решение до конца, слишком трудоёмко набирать решение на клавиатуре, а сканера увы пока нет... Решу на бумаге , выложу ответ..Удачи..:)