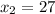прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: ).
Пусть , тогда:
Тогда:
1).
(теперь нужно представить 3 так, чтобы под логарифмом было такое число, которое с основанием логарифма будет равняться 3 (иначе говоря 3 в степени 3 (первая 3 - для того, чтобы сократить и после этого осталась чистая степень - 3)
(таким числом под логарифмом будет 27: )
(одинаковые логарифмы с основанием 3>1 - можем их убрать)
2).
(сделаем тоже самое: нужно представить 1 так, чтобы под логарифмом было такое число, которое с основанием логарифма будет равняться 1 (иначе говоря 3 в степени 1 (3 - для того, чтобы сократить и после этого осталась чистая степень - 1))
(таким числом под логарифмом будет 3: )
(одинаковые логарифмы с основанием 3>1 - можем их убрать)
Y'= (x^2-9x+9)' * e^(x-7) + (x^2-9x+9) * (e^(x-7))'= =(2x-9)*e^(x-7) + (x^2-9x+9)* e^(x-7)=e^(x-7)*(2x-9+x^2-9x+9)= =e^(x-7)*(x^2 -7x)=e^(x-7)*(x-7)*x. Приравняем в нулю. так как е в любой степени больше нуля, y'=0 при x=0 или x=7. отметим на координатной прямой эти точки 0 и 7 , проставим знаки + - + справа налево. Видно, что в точке х=0 производная меняет знак с + на минус, это точка максимума, в точке х=7 знак меняет с минуса не плюс, это точка минимума. Как раз это точка находится в заданном интервале. Подставим х=7 в исходную функцию у наим.=(7^2-9*7+9)*e^0=-5*1=-5
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: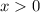 ).
).
Пусть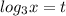 , тогда:
, тогда:
Тогда:
1).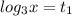
(таким числом под логарифмом будет 27: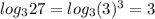 )
)
2).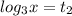
(таким числом под логарифмом будет 3: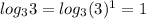 )
)
ответ: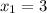 ,
,