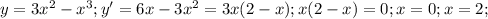сделать 4 задание по алгебре. Заранее

Question

Алгебра: сделать 4 задание по алгебре. Заранее

Nikita200111 · Accepted Answer

1)

y=3x^2-x^3; y'=6x-3x^2=3x(2-x);x(2-x)=0;x=0;x=2;

- две критические точки в области определения R.

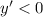на промежутках 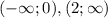$(- \infty;0),(2;\infty)$ и y'0

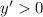на промежутке (0;2)

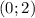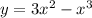, значит функция y=3x^2-x^3

убывает на промежутках 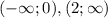$(- \infty;0),(2;\infty)$ и возрастает на промежутке (0;2)

.

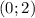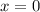- точка минимума, x=2

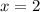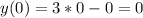- точка максимума. y(0)=3*0-0=0

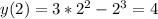- значение минимума функции, y(2)=3*2^2-2^3=4

- значение максимума функции.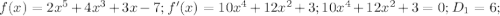
2) f(x)=2x^5+4x^3+3x-7;f'(x)=10x^4+12x^2+3;10x^4+12x^2+3=0;D_1=6;

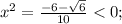$x^{2} = \frac{-6- \sqrt{6}}{10}$ - корней нет,
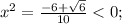$x^{2} = \frac{-6+\sqrt{6}}{10}$ - корней нет.
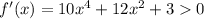итак, критических точек нет, значит в области определения R функция монотонна, т к f'(x)=10x^4+12x^2+30

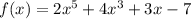при любых х, то функция f(x)=2x^5+4x^3+3x-7

возрастает в области определения R.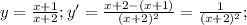
3) т к касательная параллельна прямой у=х-3, то угловой коэффициент касательной k=1.
$y= \frac{x+1}{x+2}; y'= \frac{x+2-(x+1)}{(x+2)^2}=\frac{1}{(x+2)^2};$
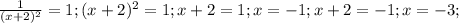
$\frac{1}{(x+2)^2}=1;(x+2)^2=1;x+2=1;x=-1;x+2=-1;x=-3;$
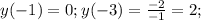
$y(-1)=0;y(-3)= \frac{-2}{-1}=2;$
(-1;0),(-3;2)

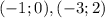- точки, в которых касательная параллельна прямой у=х-3.

MOGZ ответил