Теорема: "Если на одной стороне угла отложить равные отрезки и через их концы провести параллельные прямые, пересекающие другую сторону угла, то и на этой стороне угла отложатся равные между собой отрезки".
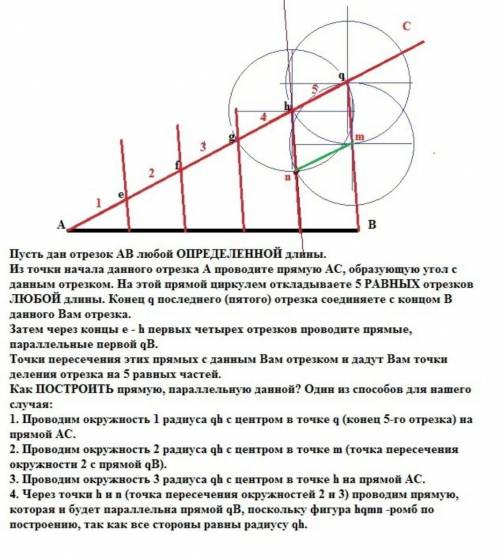
Пусть дан отрезок АВ любой ОПРЕДЕЛЕННОЙ длины.
Из точки начала данного отрезка А проводите прямую АС, образующую угол с данным отрезком. На этой прямой циркулем откладываете 5 РАВНЫХ отрезков ЛЮБОЙ длины. Конец q последнего (пятого) отрезка соединяете с концом В данного Вам отрезка.
Затем через концы e - h первых четырех отрезков проводите прямые, параллельные первой qB.
Точки пересечения этих прямых с данным Вам отрезком и дадут Вам точки деления отрезка на 5 равных частей.
Как ПОСТРОИТЬ прямую, параллельную данной? Один из для нашего случая:
1. Проводим окружность 1 радиуса qh c центром в точке q (конец 5-го отрезка) на прямой АС.
2. Проводим окружность 2 радиуса qh c центром в точке m (точка пересечения окружности 2 с прямой qB).
3. Проводим окружность 3 радиуса qh c центром в точке h на прямой АС.
4. Через точки h и n (точка пересечения окружностей 2 и 3) проводим прямую, которая и будет параллельна прямой qB, поскольку фигура hqmn -ромб по построению, так как все стороны равны радиусу qh.
(см. объяснение)
Объяснение:
Заметим, что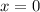
не является корнем уравнения.
Тогда поделим его на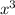
:
Выполним группировку:
Заметим, что если
- корень уравнения, то 
тоже.
Тогда единственное решение возможно, если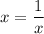
.
Иными словами, исходное уравнение может иметь ровно один корень тогда, когда
.
Подставляя
в исходное уравнение, получаем, что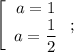 
Подставляя
, получаем, что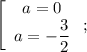 
Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.
Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.
Итого при
исходное уравнение имеет единственное решение.
Задание выполнено!