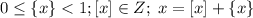Read the text.
I'm Gopher and I love sports. My favourite sport is
baseball. I play it twice a week with my friends
from school. My dad taught me a lot about
baseball. We used to practice in our garden at
home. I once broke our kitchen window and mune OST
wasn't too happy. Nowadays my dad has beco SA
quite lazy and it's hard to get him off the coy
Answer some questions for Gopher's dad:
• What sports does your father like?
Does he prefer playing them or watching,
them?
• Where does he watch (play) them?
• How often does he watch (his favourite sports)?
• Hen does he watch them?
-Gophods younger brother Max is into golf. He'd
like to become the new Tiger Woods, so he has
already started cheating on his girlfriend.
Unfortunately, his golf game hasn't improved
much seine tips to get better:
Buy better golf baits

👇

Открыть все ответы

Ответ:

hjhytu

03.05.2022

По определению,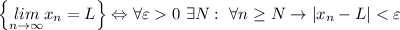 $\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение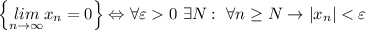 $\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

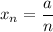
2) $x_n=\dfrac{a}{n}$

|x_n|

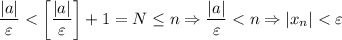
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

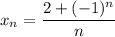
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда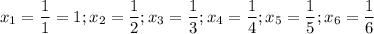 $x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$

___________________________

Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. $0\leq \{x\}$

пример 2 и 4. Все теоремы и аксиомы, будьте добры, распишите. Действий, пусть и банальных, легких не

4,6(34 оценок)

Ответ:

Злата1616

03.05.2022

Тут нужно решать интервальным методом, показать здесь я это не могу. Но для начала нужно найти нули функции(значения х, при котором функция была бы равна нулю). Здесь нули ф.: 4;-3,5. Затем чертим ось ох, обозначаем эти точки и участки, где функция положительна или отрицательна. В итоге получаем, что функция <0 при х принадлежащем отрезку (-3,5;4) 2 решается точно так же, но тут для удобства нужно в 1 скобуе поменять местами числа, затем вынести за скобки -1 и умножить обе части неравенства на -1(при этом знак> меняется на знак <). Вот что получается (х-2)(х+1)<0. Нули функции: 2;-1. Дальше как я уже объяснял выше. ответ: при х принадлежащем отрезку (-1;2)

4,8(72 оценок)

Это интересно:

Компьютеры-и-электроника

22.02.2021

Как создать аккаунт в Gmail: шаг за шагом...

Стиль-и-уход-за-собой

11.01.2023

10 способов развить чувство стиля: от выбора базовых вещей до экспериментов со стилем...

Здоровье

27.08.2022

Естественные способы лечения нарколепсии...

Образование-и-коммуникации