1). При каких значениях переменной х функция у = – х2 + 5х +3 принимает значение, равное – 9 ?
2). Постройте график функции у = х2 –+2х – 8 . Опишите все свойства:
а) область определения функции
б) множество значений функции
в) координаты вершины параболы
г) нули функции
д) координаты точек пересечения графика с осями координат
е) промежутки возрастания и убывания функции
ж) значения х , при которых у > 0; у < 0;
з)наибольшее и наименьшее значение функции.
Найдите с графика:
и) значение у при х = – 1,5 ;
к) значения х , при которых у = 3 ;
3). Не выполняя построения графика функции у = – 5 х2 + 6х, найдите её наибольшее или наименьшее
значение.
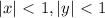
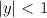 возвести в квадрат, получив,
возвести в квадрат, получив, 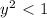 , что и требовалось проверить.
, что и требовалось проверить.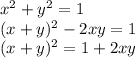
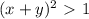
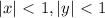 , следует, что 0 <x < 1, 0 < y < 1
, следует, что 0 <x < 1, 0 < y < 1