См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒ м
м
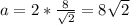 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
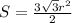 ⇒
⇒
 см
см
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
 ≈151 см²
≈151 см²
(где n - градусная мера дуги сектора)

1.
16/31 > 11/31
21/23 < 1
37/33 > 1
2.
7/27+ 16/27- 19/27=4/27
4 5/19- 2 2/19+ 7 9/19=9 12/19
1- 18/27= 1/3
6 2/9- 4 5/9= 5/3
3.
1)36:12*11=33 ученика; ответ: 33 ученика занимаются спортом
4.
16*19/8=2*19=38 ведер
5.
11/4 = 2 3/4
43/8 = 5 3/8
6.
Переведём всё в неправильные дроби, (только знаки строгие то есть не меньше или равно а строго меньше просто не нашёл как их тут поставить) далее домножим все части неравенства на 9, получим 22≤х≤28 значит натуральные значения которые будут решениями 23 24 25 26 27 так как знак строгий. а вообще ответ записывается так: х(22;28), но так как просят натуральные значения х то ответ 23 24 25 26 27.
7.
Максимальное n = 5, 5*19 = 95 < 100
8.
а=5,6,7,8,9, так как 5/5, 6/5,7/5,8/5,9/5 это неправильные дроби, 9/5,9/6,9/7,9/8 и 9/9 это тоже неправильные дроби
y=5x+4
X=0,4
Y=5*0,4+4=2+4=6
б)у=3
5х+4=3
5х=-1
Х=-0,2