Объяснение:
выражение в квадратном корне должно давать положительный результат, иначе выражение не
имеет смысла
1) √х. х не должен быть –1 или каким-то другим отрицательным числом, поэтому выражение имеет смысл при х (0; +∞)
2) √х². Здесь х также может быть и отрицательным, поскольку он возведён во вторую степень, которая даёт положительный результат в любом случае поэтому: х (–∞; +∞)
3) √–х. х не должен быть положительным, поскольку при положительном х у нас получится отрицательный итог, например при х=1 =√–1, это недопустимо, поэтому х должен быть: х≤0 и значение следующие: х (–∞; 0)
5) √25х. х должен быть 0 или положительное значение:
х≥0, поэтому х (0; +∞)
4) √–3х. х должен быть отрицательным, чтобы выражение давало положительный результат:
х (–∞; –1)
6) √0,01х, х≥0; х (0; +∞)
7)
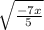
х ≥ 0; х (–∞; 0)
8)
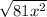
х может быть как положительным так и отрицательным, поскольку он возведён во вторую степень и значение выражения всегда будет положительным: х (–∞; +∞)
oa=oc=ob=16
получается внутри треуг abc три равноб тр.
1)в тр. oab углы при основании равны 30 гр (сл из усл.)
проведем высоту ok, онаже и медиана.
рассмотрим тр okb - прямоугольный, с гипотин. = 16 (радиус) и угол 30 гр: следует напротив угла в 30гр лежит катет в 2 раза меньший гипотенузы, след = 8.
по теор пиф. kb квадр= 16^2-8^2
=kb = корень из 192
ab= (кор192)*2
2)в тр. oсb углы при основании равны 45 гр (сл из усл.) следовател угол boc =90
с гипотин. bc
катеты =16 (радиус)
по теор пиф. cb квадр= 16^2+16^2
=cb = корень из 512
1)А(2; -1)
-1=4*2-7
-1=1
не проходит
2) В(0; -7)
-7=4*0-7
-7=-7
проходит
3) С(-1; -11)
-11=-4-7
-11=-11
проходит
4) D(-1; 11)
11=-4-7
11=-11
не проходит
5) М(7; 0)
0=4*7-7
0=21
не проходит