Решим первое неравенство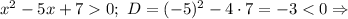 
соответствующее уравнение корней не имеет, а поскольку старший коэффициент =1>0,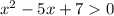 
при всех x.
Остается решить второе неравенство. Существует много рассуждения, выберем тот , который редко используется. Поскольку обе части неравенства неотрицательны, извлечение корня из них приводит к равносильному неравенству
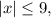
остается вспомнить геометрический смысл модуля, состоящий в том, что модуль x - это расстояние от начала координат до точки с координатой x. Поэтому ![|x|\le 9\Leftrightarrow x\in [-9;9].](/tpl/images/1855/2239/c720b.png)
ответ: [- 9;9]
1. Всего карточек 50 из них 9; 18; 27; 36; 45 кратны 9 - их всего 5 карточек.
Всего все возможных событий: n=50
Всего благоприятных событий: m = 5
Искомая вероятность: P = m/n = 5/50 = 1/10 = 0,1.
2. Всего все возможных подбрасывания игральных кубиков: 6*6=36
На желтой кости выпало четное число: {2;4;6}
На красной кости - {5}
Всего благоприятных событий: 3*1 = 3.
Искомая вероятность: P = 3/36 = 1/12
3. Вероятность того, что вынутая наугад карта окажется шестеркой красной масти равна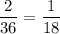
. Тогда вероятность того, что вынутая наугад карта окажется не шестеркой красной масти равна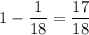 
4. Выпишем все выпадения очков, в сумме не меньше 11.
{6;6}, {5;6}, {6;5} - всего 3
Искомая вероятность: P = 3/36 = 1/12
5. Всего все возможных событий: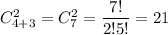
Один красный шар можно достать а один белый По правилу произведения, достать один красный и один белый шары можно
Искомая вероятность: P = 12/21 = 4/7