х (км/ч) - скорость 2-го лыжника
у (ч) - время 2-го лыжника
х+3 (км/ч) - скорость 1-го лыжника
у-2 (ч) - время 1-го лыжника
1) ху=180 путь 1-го лыжника
2) (х+3)(у-2)=180 - путь 2-го лыжника
3) ху=(х+3)(у-2)
ху=ху-2х+3у-6
ху-ху+2х-3у+6=0
2х-3у+6=0
4) Т.к. ху=180
у=180/х, подставив значение х, получим
2х-3*(180/х)+6=0
2х- 540/х +6 =0, умножим обе части ур-я на х
2х^2 +6х -540 =0
х^2 +3х - 270 = 0
D=1089
х=15 км/ч - скорость 2-го лыжника
15+3=18 км/ч - скорость 1-го лыжника
ответ: 18 км/ч
D ∈ [-5 ;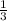 
]
Объяснение:
D (Область определения) - это все х
По условию дано: y=√(5-14x-3x²)
корень можно извлекать из числа ≥ 0
Найдём при каких значениях икс 5-14x-3x² ≥ 0:
-3x²-14x+5 ≥ 0
3x²+14x-5 ≤ 0
D = b² - 4ac = 14² - 4*(-5)*3 = 196 + 60 = 256 = 16²
= 
= 
=
= 
= 
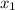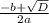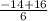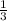
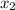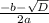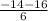= -5
Применим метод интервалов:
расположим получившиеся корни на числовой прямой
+ _ +
--------------------5----------------------------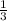---------> x
Решением этого неравенства 3x²+14x-5 ≤ 0 является [-5 ; ]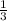
Объяснение:задание 3
-0,6z-0,6v+0,6t