ответ: x = ±√3
Объяснение:
можно двумя решить (выбирайте-какой больше понравится...)
1) 3 = (√3)²
3*(х+2)² = (√3)² * (х+2)² = ( √3(х+2) )²
получили выражение вида: a² = b² --> |a| = |b| --> a = ±b
или 2х + 3 = √3*х + 2√3 --> 2x - √3*x = 2√3 - 3 --> x(2-√3) = √3(2-√3)
x = √3
или 2х + 3 = -√3*х - 2√3 --> 2x + √3*x = -2√3 - 3 --> x(2+√3) = -√3(2+√3)
x = -√3
2) т.к. х=-2 НЕ является решением уравнения (корнем) - это можно проверить устно: (-4+3)² ≠ 3*0²,
то обе части равенства можно разделить на (x+2)² ≠ 0
получим: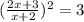 
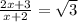или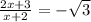 
продолжение решения аналогично 1)
или можно выделить целую часть:
--> 
--> 
--> 
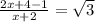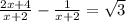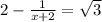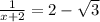
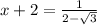
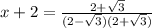
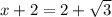--> x = √3 ( второе ("с минусом" -√3) аналогично)
8 y^2 - 7 y - 53 = 2 (4 y^2 - y + 1)
8 y^2 - 7 y - 53 = 8y^2 - 2y + 2
- 7 y - 53 = -2 y + 2
-5y =55
y = -11
Добавлю для некоторых подробное решение, с самого начала, без сокращений, с комментариями
(2y-3)(3y+1)+2(y-5)(y+5)=2(1-2y)^2+6y
Подробное решение
6y^2 + 2y - 9y - 3 + 2(y^2 - 25) = 2(1 - 4y + 4y^2) + 6y
6y^2 + 2y - 9y - 3 + 2y^2 - 50 = 2 - 8y + 8y^2 + 6y
8y^2 - 7y - 53 = 8y^2 - 2y + 2 /сокращаем 8y^2
-7y - 53 = -2y + 2 /Перенесём известные в одну сторону, неизвестные в другую
-7y + 2y = 2 + 53
-5y = 55
y = -11
неравенство. Выпишите правильный ответ.
а) х 2 + 5х = 0 в) х 2 – 2х < 7
б) – 6х – 8 > х + 3 г) х + 9 = 4х – 16
2. Выясните, решением какого неравенства является число 2.
Выпишите правильный ответ.
а) х 2 – х < 0 в) х 2 + х – 3 > 0
б) – х 2 + 4х – 5 > 0 г) х 2 – 2х < 0
3. Решите неравенство методом интервалов и выпишите
верный ответ: (х – 5)(х + 3) > 0
а)
в)
– 5 3 – 3 5
б) г)
– 3 5 – 5 3
4. Установите соответствие между квадратными
неравенствами и их решениями. ответ запишите в таблицу.
А [–6; 2]
1 х 2 + 4х – 12 ≥ 0 Б (–∞; –2] U [6; +∞)
2 х 2 – 4х – 12 ≤ 0 В (–∞; –6] U [2; +∞)
3 х 2 + 4х – 12 ≤ 0 Г [–6; –2]
4 х 2 – 4х – 12 ≥ 0 Д [–2; 6]
Е (–∞; 2] U [–6; +∞)
5. Решите квадратные неравенства и запишите полученные
ответы.
а) – 2х 2 – 5х + 3 ≤ 0 б) 3х 2 – 4х + 7 >