N, n+1, n+2 - три последовательных натуральных числа n+(n+1)+(n+2)=3n+3=3(n+1) Т.к. один из множителей произведения равен 3, то всё произведение делится на 3.
n(n+1)(n+2) Воспользуемся признаком делимости на 6: На 6 делятся числа, которые одновременно делятся и на 2 и на 3. Из трёх последовательных натуральных чисел всегда найдётся не менее одного чётного, т.е. делящегося на 2. На 3 делится каждое третье натуральное число, следовательно, из трёх последовательных множителей обязательно будет один, делящийся на 3. Получаем, что в произведении n(n+1)(n+2) один из множителей делится на 2, а другой на 3, значит всё произведение делится на 6.
N, n+1, n+2 - три последовательных натуральных числа n+(n+1)+(n+2)=3n+3=3(n+1) Т.к. один из множителей произведения равен 3, то всё произведение делится на 3.
n(n+1)(n+2) Воспользуемся признаком делимости на 6: На 6 делятся числа, которые одновременно делятся и на 2 и на 3. Из трёх последовательных натуральных чисел всегда найдётся не менее одного чётного, т.е. делящегося на 2. На 3 делится каждое третье натуральное число, следовательно, из трёх последовательных множителей обязательно будет один, делящийся на 3. Получаем, что в произведении n(n+1)(n+2) один из множителей делится на 2, а другой на 3, значит всё произведение делится на 6.
Объяснение:
a-b=6
a=6+b
(6+b)*b=5
b*b + 6*b - 5=0
b1=-3+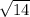 a1=3+
a1=3+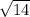
b2=-3-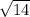 a2=3-
a2=3-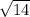
1 вариант:
(a+b)2=(2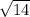 )2=4
)2=4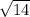
2 вариант:
(a+b)2=0