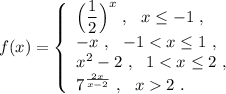
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .
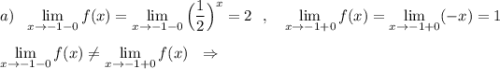
При х= -1 функция имеет разрыв 1 рода .

При х=1 функция непрерывна.
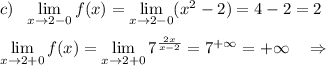
При х=5 функция имеет разрыв 2 рода .
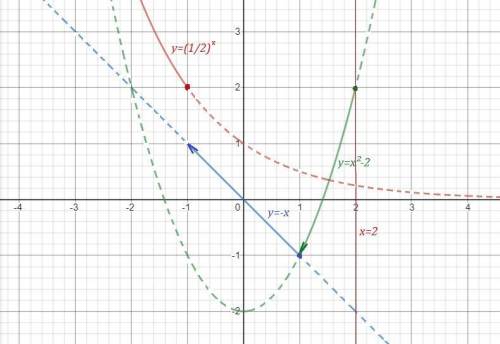
График функции нарисован сплошными линиями.
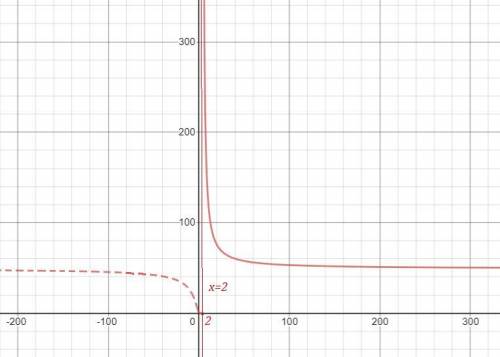
На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..
Очень сложно писать ответ, т.к. Вы просите решить сразу несколько задач.
При этом, ряд задач нечетко сформулирован, например пункт третий. Что выразить??
1. Для того, чтобы понять порядок возрастания чисел, нужно понять, что это за числа.
Для этого, возведем каждое число в квадрат, тем самым избавившись от корней.
а= 2 в квадрате умножить на 5 = 4*5=20
б = 3 в квадрате умножить на 2 = 9*2=18
в = 21
Итак, числа в порядке возрастания будут выглядеть так: в,а,б.
(ну или можете их написать теми величинами с корнями, что даны в задании, как Вас учат?)
6. Выражаем Икс через Игрек и подставляем во второе уравнение.
Дальше решаем.
Итак,
7х-3у=34
5х-6у=8
Х = 34+3у разделить на 7
теперь подставим
5*(34+3у)/7 -6у = 8
решаем
(170+15у)/7-6у = 8
умножу все на 7, чтобы избавиться от дроби
170+15у-42у=56
27у=114
у=114/27=4,22