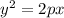ее фокус находится в точке с координатами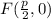 
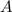находиться в системе уравнения 
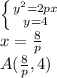Если уравнение касательной равна 
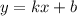с учетом того что она проходит через точку получаем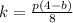 
, подставляя 
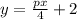
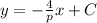он проходит через точку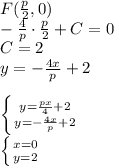 
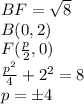
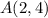
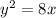
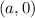центр окружности (так как центр лежит на оси 
) 
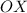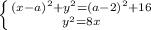
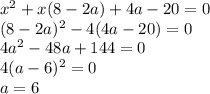
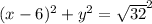
y = x4 – 8x2 + 5
1.Найдем точки экстремума функции, т.е. точки, в которых y’ = 0:
y’ = (x4 – 8x2 + 5)’ = 4x3 – 16x.
4x3 – 16x = 0;
4х (х2 – 4) = 0;
4х (х – 2) (х + 2) = 0;
х1 = 0;
х2 = -2;
х3 = 2.
2. Промежутку [-3; 2] принадлежат все найденные точки, поэтому рассмотрим значение функции на концах отрезка и в точках экстремума.
При х = -3, у = 81 – 72 + 5 = 14.
При х = -2, у = 16 – 32 + 5 = -11.
При х = -0, у = 5.
При х = 2, у = 16 – 32 + 5 = -11.
Таким образом, yнаим = у(-2) = у(2) = -11, yнаиб = у(-3) = 14.
ответ: yнаим = -11, yнаиб = 14